D3DXMATRIX R, T, M;
D3DXMatrixTranslation(&T, 2.0f, 0.0f, 0.0f);
D3DXMatrixRotationY(&R, -D3DX_PI*0.5f);
M=R*T;
M=M*SomeOtherMatrix;
D3DXMatrixInverse(&M, NULL, &M);
float r=GetYRotation(&M); // the helper I want to make
// if it worked properly it would do this:
D3DXMatrixRotationY(&R, D3DX_PI*0.5f);
float r=GetYRotation(&M);
// r would equel pi*0.5
if the M matrix will always be Y rotation matrix, you could derive the parameter it is constructed from just as this : acos (M[0][0]).
But this parameter is not an angle with Y axis - it is actualy an angle in ZX plane - thus making objects revolve around Y axis if transfomed by M.
But if you will incompose also Z and X rotation matricies into the M matrix (multiply the M with them), then you will not be able to use this simple solution. You will need to solve 3 linear equations. I recomend Cramer method for solving them as it does not use division, so you will be zero safe. Following is a method that constructs world rotation and translation from the 3 axises sinuses and cosinuses and position
function ComposeWorld4x3(cx,cy,cz,sx,sy,sz,x,y,z,res,offr)
{
var m1=cy*cz;
var m2=cy*sz;
var m3=-sy;
var m4=sx*sy*cz-sz*cx;
var m5=sx*sy*sz+cx*cz;
var m6=sx*cy;
var m7=cx*sy*cz+sz*sx;
var m8=cx*sy*sz-sx*cz;
var m9=cx*cy;
res[offr]=m1;
res[offr+1]=m2;
res[offr+2]=m3;
res[offr+3]=0.0;
res[offr+4]=m4;
res[offr+5]=m5;
res[offr+6]=m6;
res[offr+7]=0.0;
res[offr+8]=m7;
res[offr+9]=m8;
res[offr+10]=m9;
res[offr+11]=0.0;
res[12+offr]=x;
res[13+offr]=y;
res[14+offr]=z;
res[15+offr]=1.0;
}
the res is a 16 array in column memory layout (res[3]is 4th component of first column) and cx,cy,cz,sx,sy,sz are cosinuses of X,Y,Z and sinuses of X,Y,Z angles respectively
Now if you look at it you may take equations as those:
var m1=cy*cz;
var m9=cx*cy;
var m3=-sy;
you should find out cy through third simple equation m3=-sy such as sqrt(1.0-asin(-1.0*m3)) and use 2 linear equations system only:
M[0][0]=cy*cz;
M[2][2]=cx*cy; where cy is aleary existing constant you computed
this is cramer's rule
Consider a system of n linear equations for n unknowns, represented in matrix multiplication form as follows:

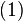
where the n by n matrix  has a nonzero determinant, and the vector
has a nonzero determinant, and the vector  is the column vector of the variables.
is the column vector of the variables.
Then the theorem states that in this case the system has a unique solution, whose individual values for the unknowns are given by:

where  is the matrix formed by replacing the ith column of
is the matrix formed by replacing the ith column of  by the column vector
by the column vector  .
.
So you would perform b column to be M[0,0],M[2,2] and A matrix to be
[cy,0]
[0,cy]
you then compute x1 and x2 by applying last sentence of quoted Cramer's rule on them both. You will then poses cx,cy,cz and use acos on all three to know angles around all three axises of a rotation matrix



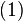
 has a nonzero determinant, and the vector
has a nonzero determinant, and the vector  is the column vector of the variables.
is the column vector of the variables.
 is the matrix formed by replacing the ith column of
is the matrix formed by replacing the ith column of  .
.

