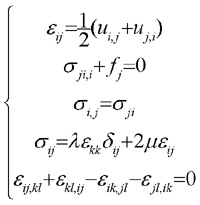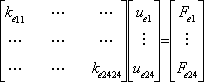[size="5"]Introduction

[size="3"]Physical Simulation

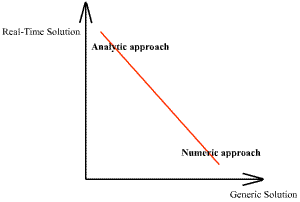
Two tools - Analytical and Numeric methods

In a few years, an important gap has been filled by the video game industry. Now the GPU and hardware computation have replaced the CPU and software emulation. But several progress axes remain very little explored by video games, like AI or physical simulation, though paradoxically these fields were studied first at the beginning of the computer age.

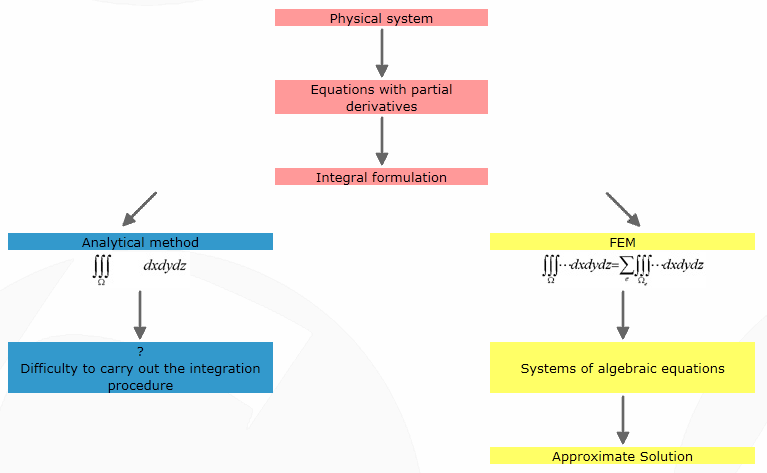
Let us take the case of the physical simulation. Before the middle of the twentieth century, physicians have set up a lot of analytical equations for many classic physical problems. But unfortunately, solutions to these equations resolved only simple cases. For example, what is called Strength of Materials has resolved some problems to calculate deformations, but applications have a small scope (i.e. cases of study). When computer started being used, analytical equations allowed finding approximate solutions; it was the beginning of the numerical computation.

The use of numerical methods enables the engineer to expand his ability to solve practical design problems. He may now treat real shapes as distinct from the somewhat limited variety of shapes from simple analytic solution. In the same way, he needs no longer force a complex loading system to fit a more regular load configuration in order to conform to a purely academic situation. Numerical analysis thus provides a tool with which the engineer may feel freer to look for the solution of problems that he faces in practice.

Two pitfalls - Real-time and Generic solutions

The application of these engineering tools cannot be adapted to the video games because:

• On one side, interactive virtual world must simulate a large variety of physical problems, each problem being different. For example, the player throws a stone in a closed room and the stone moves according to the starting velocity, the geometry of the room and player's orientation and position. Moreover this depends on random events like stranger compounds interfering. Analytical solution of the stone throw differs each time, so the only choice consists in computing the displacement step by step. Consequently, setting up an analytical formula of a physical phenomenon reduces the computation time due to the factorisation, but this formula is very difficult to elaborate.
• On the other side, the numerical computation, often iterative, is rarely possible in real-time. The computation takes several minutes, sometimes hours or days to solve engineering problems. It is then impossible to achieve simulation in real-time especially for video games.

Two notions - Realistic and Real solutions

The last aspect of the physical simulation is the duality between the realistic appearance and the real. A real solution is an correct solution. In such case we admit that a solution is correct when the difference between the theory and the solution found is negligible in comparison with the dimension of the physical problem.

A realistic solution seems to be physically correct. It is a relative notion, which depends on the observer. If a player throws a stone, and if the reality differs from the solution by several centimetres, the player has seen the stone bouncing from the wall/s and he has admitted that the path is right.

That is why particle systems are very used in video games. In this case, the simulation is not physically correct but is realistic. Simplifying the reality is not a problem if the results are realistic.

[size="3"]Objectives of this article - Study the deformation of solids in real-time

In this technical article, I have opted to concentrate on elements that haven't been really studied in the game industry. So I have selected the deformation of solids i.e. steel or concrete structures. Deformations of solids could occur in many occasions during a game for example when a car crashes into a wall, or the player fires a rocket into a structure.

Main specifications

I am going to explain how to build a simulation with the following features:

• In real-time;
• Obtain realistic solution;
• Manage a large variety of shapes for the body;
• Apply various boundary conditions.

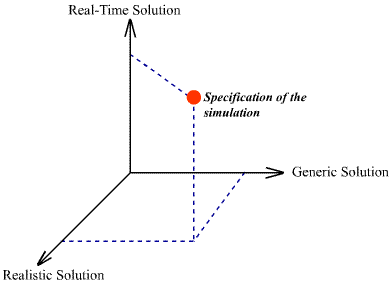
Specifications of the simulation

Besides the only tolerated hypothesis is that the deformations always occur in the elastic domain, i.e. there is a linear relation between the applied forces and the displacements.

I know the specifications are ambitious and seem to be contradictory. Nevertheless, I will explain further how to mix multidisciplinary fields to achieve my goals:

• [alink='1']Preliminary discussion[/alink]. Some technical terms and hypotheses are defined.
• [alink='2']Finite Element Method[/alink]. I present the core method used to meet the specifications.
• [alink='3']Adaptation of the FEM[/alink]. This method, like a lot of others, must be adapted.
• [alink='4']Appendix[/alink]. Relevant links and resources about the subject.

Foreword

A project, called Hyperion Project (see the part bellow), illustrates the subject of the article. Moreover all the sources are licensed under LGPL (Lesser General Public License). See http://www.gnu.org for more information about the license.

I let an important liberty on the complete source:

• to prove that the explained method is not so complex;
• to promote the method in the video games industry.

[size="3"]The Hyperion Project

Component Technology

The notion of binary components and oriented object design are one of the interesting subjects in the programming and conception field. During the year 1999, I worked for an industrial software company specialised in real time and embedded systems. There, I developed a mechanism close to Component Object Model by Microsoft and adapted for Unix, Windows and VxWorks operating systems.

This system was re-adapted for the kernel of Hyperion to obtain a set of classes, which allows to create very quickly Hyperion components. This new framework has been called Hyperion Pattern. This framework has been designed for environments supporting dynamic libraries.

Library of specialised components

With the help of this framework, the applications could be not only object oriented but also could be component oriented. Moreover I am open-minded to many aspects of engineering subjects, especially analytical mathematics and mechanical engineering. So in order to test on a large scale the new developed framework, I created the first components specialised in the physical simulation in real-time. The long-term prevision is to set a coherent and dense library of components in the same way as Direct X, which is specialised in the multimedia.

Ephydryne components

The Ephydryne Components compute the deformation of solids and so realise the specifications explained in the previous part. The Ephydryne package defines a set of interface and implements the necessary components to make all the necessary computing steps.

State of the realization

To prove the capabilities of the Ephydryne components and the viability of the chosen solutions, two client applications have been developed:

• HypDev;
• HypVisual.

[nbsp][nbsp][nbsp][nbsp]

HypDev and HypVisual are considered as demonstration products because the Ephydryne Components are the core of the project.

Go to http://sourceforge.n...ects/ephydryne/ to download sources and documentation.


[size="5"][aname='1']Preliminary discussion

[size="3"]Some definitions

Hypothesis of continuity

The basic structure of the matter is characterized by non-uniformity and discontinuity attributable to its various subdivisions: molecules, atoms and subatomic particles. The concern in this document is to replace the actual system of particles with a continuous distribution of matter. There is the clear implication in such an approach that any small volumes which could be considered here are enough to contain a lot of particles. Random fluctuations in the properties of the material are not considered to be important.

Definition of the studied system

The studied system is a solid, which is sometimes referred to by the name of body. Some of the main abilities of a solid are:

• to maintain its shape without need of a container;
• to resist continuous shear and tension.

Mechanics of solids

In contrast with rigid body statics and dynamics, which treat the external behaviour of bodies, the mechanics of solids are concerned with the relationship of external effects (i.e. forces and moments) to internal stresses and strains.

Types of strains

External forces actions on a body may be classified as surface forces and body forces. A surface force is of the concentrated type when it acts at a point; a surface force may also be distributed uniformly or non-uniformly over a finite area. Body forces act on volumetric elements rather than surfaces and are attributable to fields such as gravity and magnetism.

Units

All the units follow the international standard (IS).

DataDimensionSymbolLengthMetermForceNewtonNPressurePascalPaMasseKilogramkgThe right-handed system is used by default.

Right-handed system

[size="3"]Which method to use?

Aim of the project

According to the first part of this document, the first target of the Hyperion Project is to calculate the deformations of a solid with a distribution of forces. As above the main specifications impose the following conditions for the simulation:

• Real-time;
• Realistic solution
• Generation of a large variety of shapes for the body;
• Application of usual boundary conditions;
• Elastic hypothesis

Analytical vs. Numerical methods

So what are the classical means to calculate the system deformations? To succeed in this task, classic analytical methods used in the mechanics of solids are limited. Strength of Materials has resolved some problems but they are too specific. Navier relations for plates and shells are also not enough generic. In conclusion, the analytical methods seem to be less adapted than the numerical method.

Nowadays, the most powerful method to resolve physical problems is a numerical method called the Finite Element Method (FEM).


[size="5"][aname='2']The Finite Element Method (FEM)

[size="3"]Introduction

The efficient finite element method originates in the 1950's and with the widespread use of the digital computers has since gained considerable favour compared to other numerical approaches. This method allows to foresee stress and strain in an engineering structure, with unprecedented ease and precision. In this article, we only discuss about continuum mechanics and its applications in the FEM.

The general procedure of the finite element and conventional structural matrix method are similar. Consequently, I am going to present this method first as it easier to understand than the FEM.

[size="3"]Structural Matrix Method

This method allows to calculate the displacement and the stress in a structure usually made of beams. The structure is idealized as an assembly of structural members connected to one another at joints or nodes at which the resultants of the applied forces are assumed to be concentrated.

Employing the mechanics of solids or the elasticity approach, the stiffness properties of each element can be ascertained. Equilibrium and compatibility considered at each node lead to a set of algebraic equations, in which the unknowns may be nodal displacements, internal nodal forces, or both, depending upon the specific method used.

In the displacement or so-called direct stiffness method, the set of algebraic equations involves the nodal displacements. In the force method, the equations are expressed in terms of unknown internal nodal forces. A mixed method is also used, in which the equations contain both nodal displacements and internal forces.

A simple model

One of the simplest cases from the structural matrix method is to idealize each member of the structure by a spring. The stability of an elastic spring is characterized by its constant of rigidity 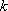. This constant is used to calculate the return force .

Spring fixed at its base

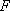The relation linking displacement and force is:

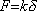
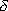is the relative length variation of the spring.

When two axial forces are applied to the spring, the stability commands that:

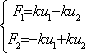
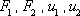are respectively the forces and the displacements for each node.

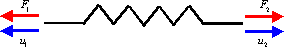
Axial forces applied to the spring

A matrix relation could replace these equations:



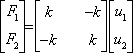
The matrix, which links the force vector and the displacement vector, is called the stiffness matrix of the spring.

We could assemble several elements modelized with springs to construct more complex structures, like this following example.

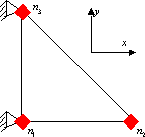
Structure made of three spring-elements

After assembling the three stiffness matrices of the element, a linear relation that links the forces and the displacement is found:

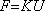
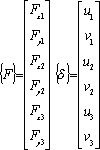
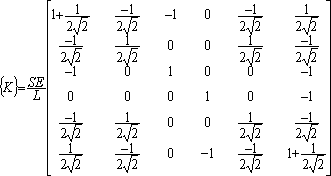
S is the section of the element

E is the Young modulus of the material

Notice that the problem has 6 unknowns (3 nodes free along the x and the y axes), which are organized in the vector.

To resolve the problem, we apply boundary conditions: the nodes 1 and 3 are fixed in the three directions. After resolving the displacements of the node 2, the reaction forces, which are applied on the nodes 1 and 3, are found.

Refer to the [alink='4']bibliography[/alink] for more information about the structural matrix method.

General relation

The fundamental relation that must be remembered is the matrix relation 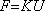. As we are going to see, with the finite element method, theses relations could be computed for any continuous body and so not only for structures.

[size="3"]Principles of the FEM

In contrast in the foregoing approaches, in the finite element method, the solid continuum is divided into a finite number of elements, connected not only on their nodes, but along the hypothetical inter-element boundary as well. In addition therefore to nodal compatibility and equilibrium, as in conventional structural analysis, it is clear that compatibility must also be met along the boundaries between the elements. Because of this, the element stiffness can only be approximately determined in the finite element method.

As in the structural analyses previously cited, there are several approaches for the FEM. In this article, we treat only the commonly employed finite element displacement approach.

Theory

Let us take a stress analysis problem for a body under certain loading conditions.

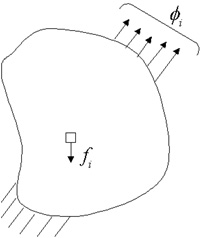
Problem characterized by its geometry, its force loading and its boundary conditions

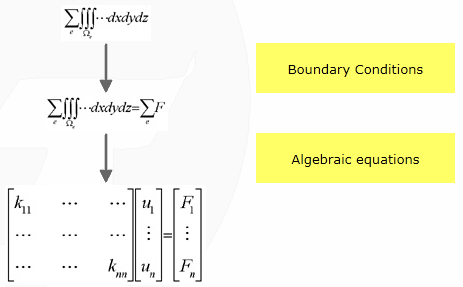
The normal analytical procedure would involve taking an extremely small box element of dimensions (dx, dy, dz) each tending to zero and then writing down the equations of equilibrium and compatibility for this element.

Then we would try to obtain a solution for the stress distribution in the body under the specified boundary conditions using the integration techniques over the entire body. The drawback of this method is that for complicated bodies it will be very difficult and sometimes impossible to carry out the integration procedure over the entire body.

The solution to such problems can be obtained very effectively and to a high degree of accuracy using Finite Element Method. Instead of assuming a displacement field for the entire body, we divide the body into smaller elements and assume a displacement field for these individual elements. The original body or structure is then considered as an assemblage of these elements. Once again, these elements are connected to each other at joints called nodes or nodal points to form the entire structure. These individual elements are now analysed. Instead of carrying out integration over the entire body consisting of infinite number of elements of infinitesimally small dimensions, we carry out summation over the body consisting of finite number of elements of finite dimensions. By this iterative approach, the method can be effectively implemented in a computer program.

The equations of equilibrium for the entire structure or body are then obtained by combining the equilibrium equation of each element so that the continuity is ensured at each node. The necessary boundary conditions are then imposed and the equations of equilibrium are solved to obtain the required variables such as stress, strain, temperature, distribution or velocity flow depending on the application.

The solution, divide to rule

We must also realize that FEM is a numerical technique and the answers obtained are not the exact solutions but only approximate. However by using appropriate procedures and proper computing facilities, we can obtain an extremely high degree of accuracy which is very much acceptable in practice. Notice that the "acceptable" term is used for engineering problems. In the video games field, after using acceptable procedures, the result can be considered physically correct.

Consequently, the structural matrix method is very close to the FEM. Actually the divided structures of beams are replaced by continuum solids.

Stiffness matrix

Previously, the stiffness matrix of a spring has been examined above. The finite element method works with more complicated element in two or three dimensions.

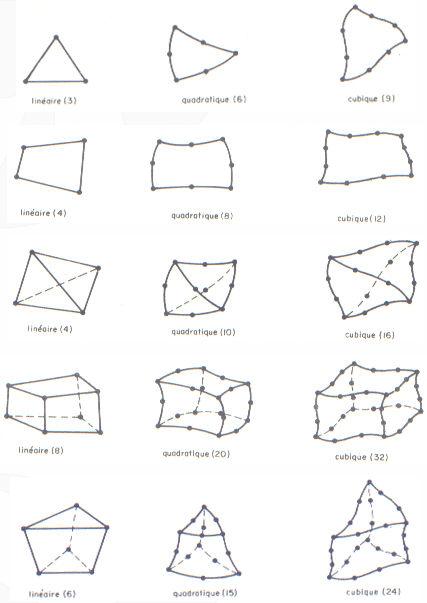
Example of finite elements (from An Introduction of the finite elements by Dhatt and Touzot)

In the project, the only used element is a cube made of eight nodes with three degrees of freedom by nodes. In fact, each node could move along the x, y and z axes. In the previously example with the spring, the nodes located at each extremities of the element can move only along the axe of the spring.

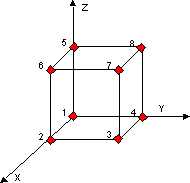
The cubic element used for the project


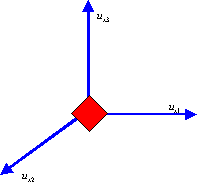
Three degrees of freedom by node

Consequently, the dimension of the stiffness matrix of this element is 24 by 24:

The matrix depends only on the material properties and dimensions of the cube. The analytical form has been calculated with Maple. The result and the Maple file is included in the attached resource file.

Refer to [alink='4']bibliography[/alink] to know how to compute stiffness matrices.

[size="3"]Common applications of the finite elements method

FEM has a wide range of applications as follows:

• Stress Analysis;
• Heat Transfer;
• Fluid Flow;
• Torsion Analysis;
• etc.

Some pictures, showing the capabilities of this method, follow.

Stress in the frame of a bike

Deformation of a dam

In this article, I will demonstrate that it is possible to adapt these industrial cases for the video games. These potential cases follow below:

Turret (from Half-Life SDK)

[size="5"][aname='3']Adaptation of the FEM

[size="3"]General procedure

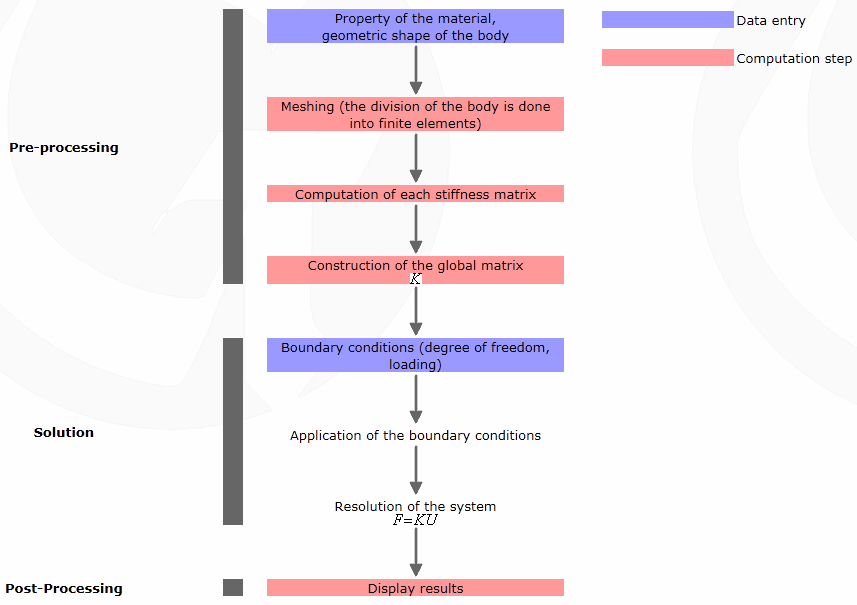
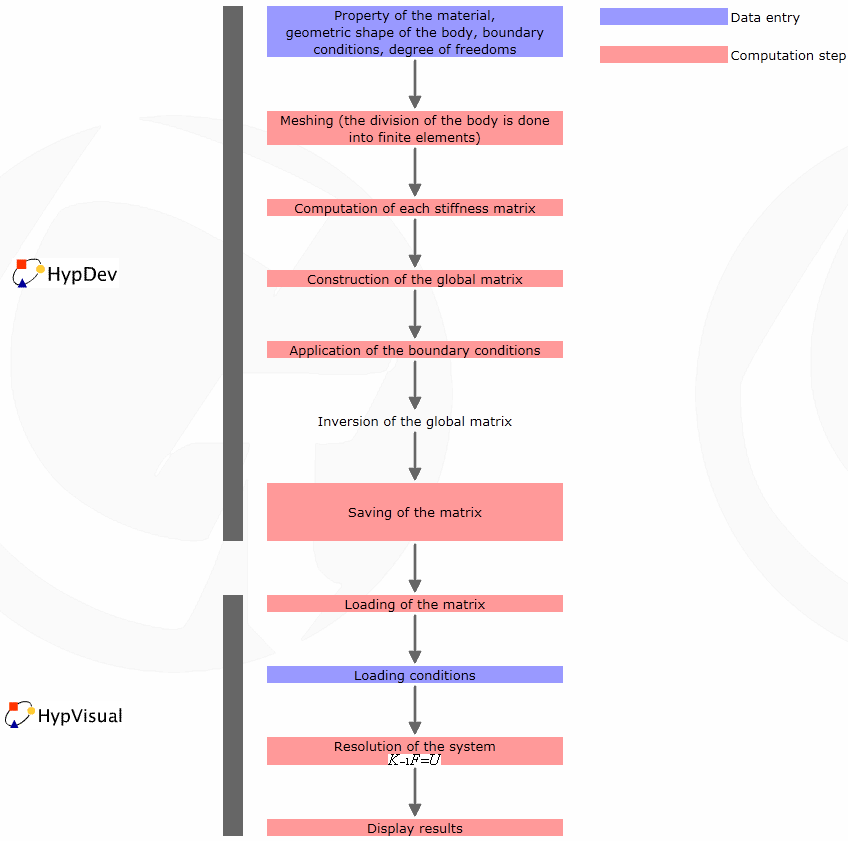
Here are the common steps for a calculation based on the FEM:

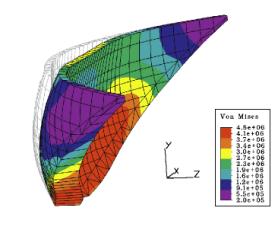
[size="3"]FEM in real-time

In current applications displayed in the previous pictures, the number of nodes and consequently the number of unknowns are very important. To find the displacements of the nodes, we must resolve the linear system 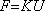. depends only on the geometry, the characteristics of the material, the number and the shape of the finite elements. Consequently, and it is the most important, the matrix doesn't depend on the applied forces.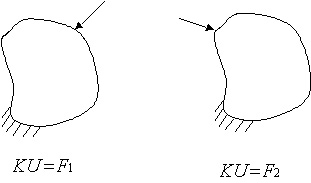

K doesn't depend of the loading conditions

To resolve the matrix system, finite element applications use Gauss elimination, substitution or Newton-Raphson methods. These methods manipulate the second member of the equation (i.e. force vector 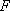), and of course these methods are the fastest. For example, the computation time to resolve a system within 10 000 degrees of freedom is about one minute. Of course it is not in real time. Let us try another trick to resolve the system. This trick is to resolve the system independently of the force vector.

Resolution in two steps

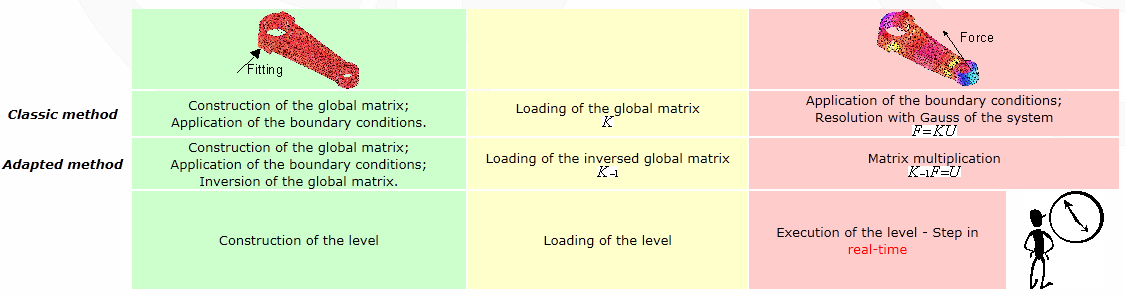
The solution is to compute the inverse of the matrix. But everyone knows that the inversion of matrix is a slow computation, but does it matter? If the solution doesn't depend on the force vector, the system is resolved before the beginning of the application. In more precise terms, the inverse of the matrix is stored in a file and loaded during the initialization of the application (typically during the loading of a game level).

The drawback of this method is that the boundary conditions are fixed and could not change. In fact, to inverse the matrix, simplification is done according to the boundary conditions. In the next part, called Study of a case, the detailed procedure will be explained.

[size="3"]Two steps and two tools

In a part of the introduction called "Hyperion Project", some units have been presented. The most important is the set of components called Ephydryne Components. These components have been developed with the Hyperion Pattern framework. The Ephydryne package defines a set of interfaces and implements components to make the appropriate computing steps of the finite element method. Two tools have been set up to use the capabilities of the Ephydryne Components.

HypDev

It is a client application that uses the Ephydryne components. The goal of HypDev is to calculate the linear relations between the forces applied on the rigid bodies and the deformations. According to the method presented in this article, the linear relation is computed during the development of the level. Again the linear relation is consequently loaded during the execution of the level. So an important part of the computation is not done during the game (step which is in real-time).

HypVisual

The step which is in real time is studied with the application called HypVisual. This application loads the file generated by HypDev, displays the body and manages the simulation.

Here are some screenshots from the application:

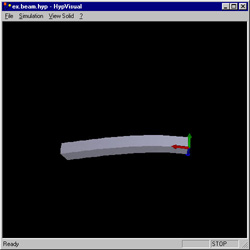
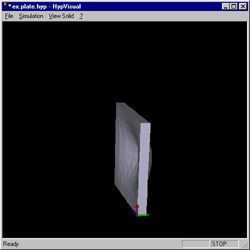
The two tools used the same set of components

For more information about these two applications, go to the web site of the project at http://sourceforge.net/projects/ephydryne/.

Here below is summarized the general process of the method:

[size="5"][aname='4']Appendix

[size="3"]Bibliography

Structural approaches

The structural approach is comparable in some ways with some computing methods, famous in the field of the video games. The most interesting articles are:

2D Surface Deformation by Max I. Fomitchev http://www.gamasutra.com/features
Devil in the Blue-Faceted Dress: Real-Time Cloth Animation by Jeff Lander http://www.gamasutra.com/features

Some other interesting resources could be found:

Site collected resources about particle systems http://www.particlesystems.com
Game which used the structural approach to find stress in bridges http://www.bridgebuilder.de

Finite Element Software

Web site of the ANSYS software http://www.ansys.com
Web site of the ROBOT software http://www.robot97.com
Web site of the C Mold software http://www.cmold.com

Resources about FEM theory

Web Site, called FEMUR, about the FEM (FEMUR = Finite Element Method Universal Resources) http://femur.wpi.edu
The Finite Element Method in Engineering Science O.C. Zienkiewicz - Mc Graw Hill - 1967
FEM/BEM Notes P. Hunter, A. Pullan - Department of the Engineering Science, University of Auckland - 2001
Accurate Real Time Deformable Object by D.L James and D.K Pai - Univeristy of British Columbia

[size="3"]Stiffness matrix of a cube with eight nodes and three degrees of freedom by nodes

Expression of the matrix hyp.stiffnessmatrix.txt (see attached resource)
Maple file used to obtain the matrix hyp.stiffnessmatrix.mws (see attached resource)