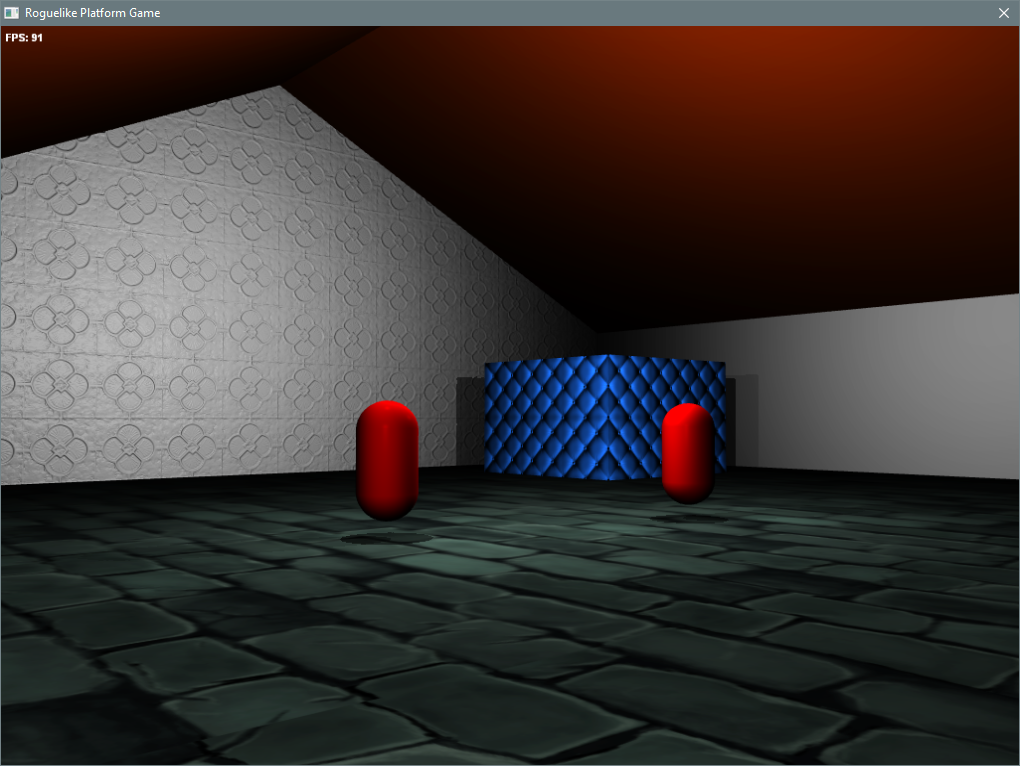
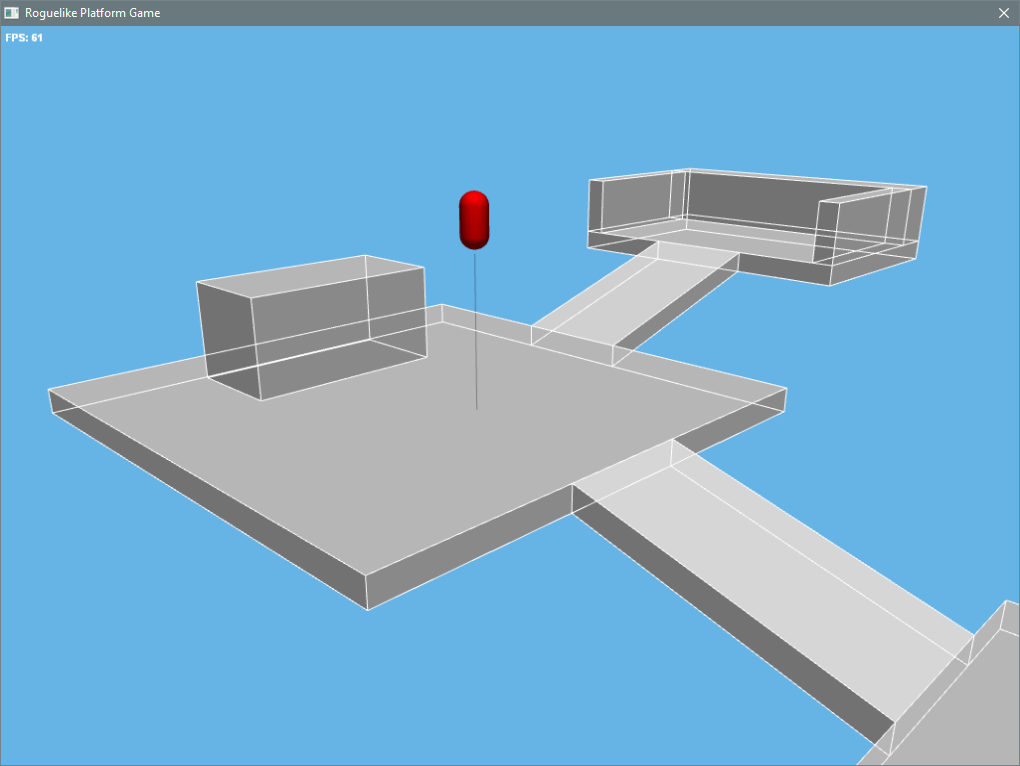
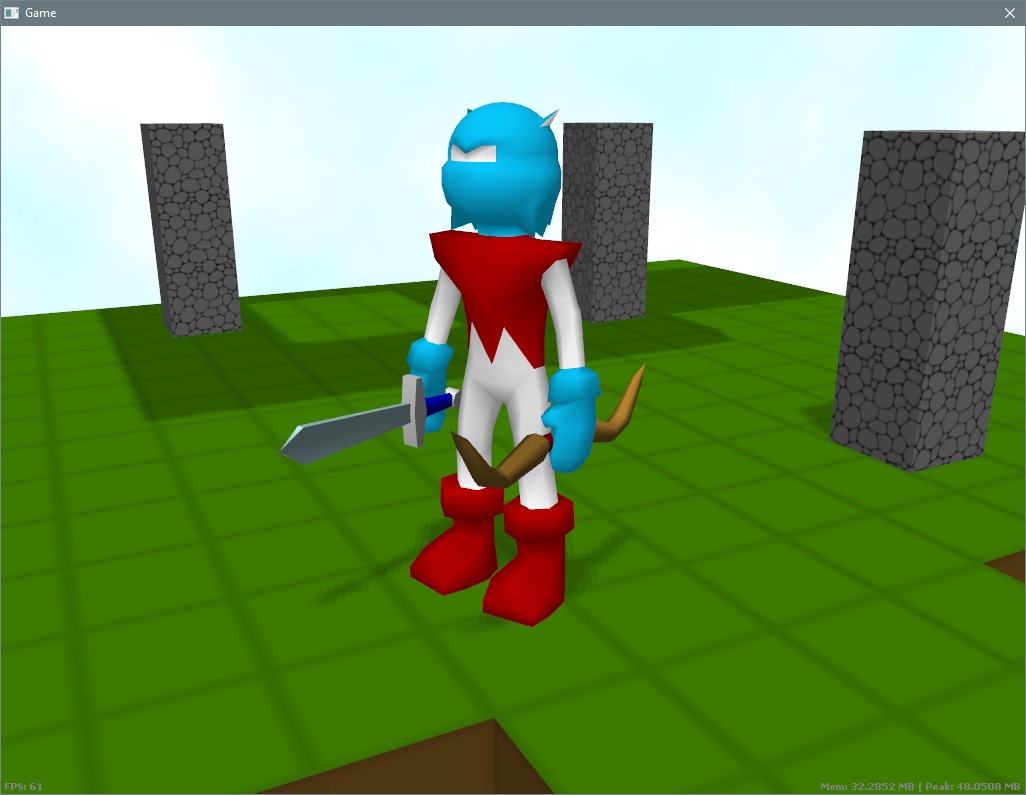
Wow. Been a while. Must be years since I last updated this. So I'm still alive and I'm working on a toy version of LLVM purely for my own amusement.
Pv is a virtual machine executable that executes a fairly small virtual instruction set:
enum class Reg : std::uint8_t
{
Pc,
Bp,
Sp,…

Been working hard on Om and added a few new features.
Figured out a way to have implicit [font='courier new']this[/font] in functions, as long as they are defined inside the object of which they are methods. Name lookup rules similar to C++, so a parameter or a local variable is considered first, th…

I seem to have become obsessed with Om, my scripting language, again and have done nothing whatsoever on my game since last entry, just been busy with Om. I justify this on the basis that a) I'll need a scripting language for my game and b) this is hobby stuff so I can do whatever the hell I like :…

Decided I needed a break from graphics programming so decided to revisit Om, my scripting language. For those who didn't read the entries about this a few months ago, I came heavily unstuck in my last iteration of this project, since I had decided to implement deterministic destruction in a dynamic…

tl;dr: health much improved, wrapped [font='courier new']QtScript[/font] in a command line application with a DLL plugin system.
When I was messing around getting normal mapping working recently, I decided to use the alpha channel of the normal map as a specular value to allow for per-pixel specular…

tl:dr; collapsed in the street, spend a night in hospital. Transparent rendering works. Character controller works. Animation works. Have a first person arm-rig sort of working.
I'll start with a personal note - collapsed in the street last Wednesday and discovered I couldn't get up. A couple of ver…
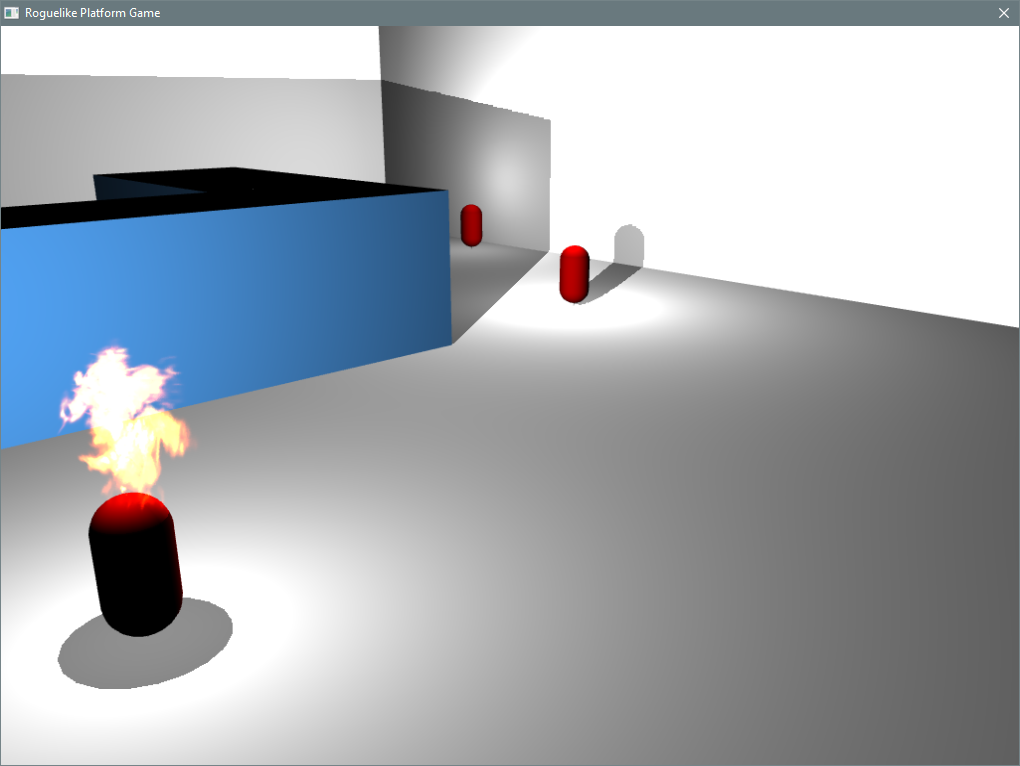
This is more of a design ramble than a technical issue that I have today. I was hoping to take the approach of having multiple point lights in my game levels, but just use a single shadow caster, but as you can see from the screenshot, this creates some weird situations where a shadow can be cast d…
Making some decent progress on the game over the last few days.
First up, I implemented a billboard-based particle system, used for the torch effect in the video above. It uses the following sprite atlas that I stole from the internet somewhere and generates a dynamic vertex buffer each frame. Since…

As always happens when I'm starting a new game, I've started a new level editor. This one, however, is based on my [font='courier new']Gx[/font] and [font='courier new']QGx[/font] frameworks and so I'm hoping to keep it generic enough that it might be the last one I ever have to write (yeah, right)…

Time for the next gripping installment of the development of my [font='courier new']Gx[/font] game framework library. The latest addition I'll waffle about today is the [font='courier new']Gx::Camera[/font] class from [font='courier new']GxMaths[/font].
The requirement I have for the camera is that…

Having made a good start on [font='courier new']Gx[/font] and having set up a game project that links to the [font='courier new']Gx[/font] headers and lib (in-place in the [font='courier new']Gx[/font] project for ease of update), I realised that a new game will need a new level editor, which for m…

About time I posted an update here. Been a while.
I have kind of lost a bit of heart in Om, my scripting language, since I realised that circular references lead to memory leaks unless I implement some kind of garbage collection. I've not given up on it - I will indeed try at some point to add GC t…

Thought I'd try blogging about this before I started implementing anything to try to get it straight in my head. I've decided to change how the Om module system works a little, based on playing around with writing a driver to allow me to execute Om scripts from within Windows explorer.
At the momen…

I've decided to just postpone worrying about cycles and memory leaks in Om for the time being. I may have to address this in the future, but for now I've discovered that there are actually so many things the user can do that cause leaks, infinite loops, stack explosions etc that I cannot efficientl…

I realised today why JavaScript doesn't have deterministic destruction. Thought I was so smart basing Om around it.
Cycles.
If one object A references an object B and B references A, Om will never release the entities when they go out of scope. Memory leaks.
This is a well enough studied problem to…

The Om Programming Language :)
Rather a long journal entry today. I hope that someone sticks with it as I'm really getting quite excited about how my scripting langauge is starting to develop now.
I started trying to write a general overview of Om last night as I've been posting about my scripting …

Following on from my last entry where i "discovered" you could use templates to provide a common interface to two unrelated classes, I've now implemented this technique in Om, my scripting compiler and virtual machine and thought I'd just write this up a bit.
Om has various [font='courier new']Om::…

Howdy.
Been quiet for a while but have been getting back into my scripting language compiler/virtual machine. No particular reason, just has grabbed my attention for the last few weeks.
Today I started adding support for range-syntax on strings and lists:var s = "hello";var m = [ "one", 2, 3.0 ]; o…
![Bow and Arrow beginnings [updated]](https://uploads.gamedev.net/blogs/monthly_11_2016/blogentry-98449-0-05560500-1478334455.jpg)
I've been working a little bit on the view mode with the bow this week. Not spent a lot of time on it but Saturday morning seems to be a good time to update my journal since I have an hour to work on the game and can't really get into anything else properly, so we are only about half-way through th…

Now I have a chase camera working that can be assigned to move to different targets, I've been working on a "view mode" for the player. Holding down the right-mouse button moves the camera to a shoulder-view mode so the player can look around.
Read more
in Journal of Aardvajk
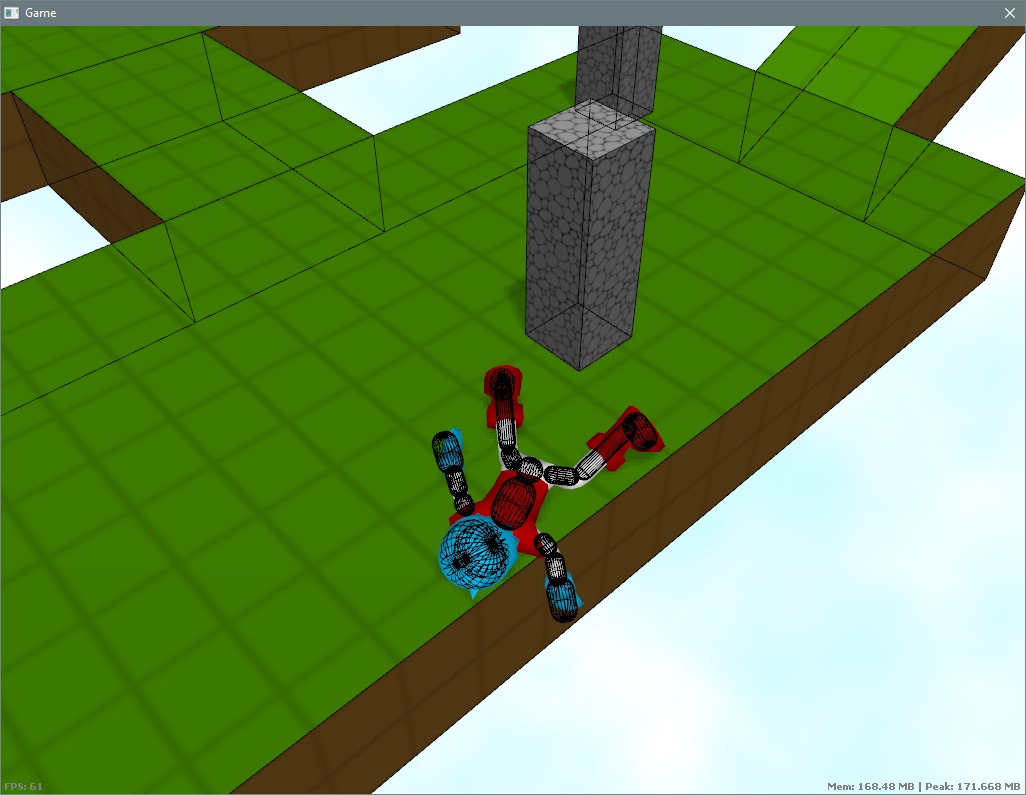
Just a quick post to say I've re-integrated my rag doll system back into the current iteration of the game. This is based on making a set of Bullet shapes from the current skeleton configuration on the fly, then handing control of these over to Bullet.
New feature here is that the new chase camera …

In preparation for being able to do some stuff with the bow aiming, I've ripped out and rewritten the [font='courier new']Camera[/font] system for the game. I've split what was one system into two classes now, [font='courier new']ViewTransform[/font] which represents a position and orientation for …