I'm talking about the sprites traveling along somewhat arbitrary curves, meaning curves that look good, not curves that result from gravity or other physical forces. If you need those kinds of curves, e.g. the parabolic trajectories of cannonballs, you need to simulate the forces acting on the sprites and that is not what I'm talking about in this post.
Caveat aside, an arbitrary curving path is a pretty common thing to need but I think is unnecessarily headache-inducing because curves in graphics are just confusing. Maybe you've found yourself thinking
- I don't know what the difference between a spline, a bezier curve, a bezier curve of various degrees, a B-spline, a t-spline, etc. is.
- I don't know which of the things mentioned above I need.
- Every time I try to read the wikipedia article on these things the math gets heavy and my eyes glaze over
etc.?
So assuming it's not just me, as a public service I'm going to try to clear this up.
Short version, if you need to have a sprite that travels along a curving path from point A to point B in x amount of time, you probably need a cubic bezier curve and generally, in 2d game programming, all you will ever need probably is n cubic bezier curves possibly concatenated together. You can concatenate them yourself if you need to do that, so what you need is a way to define a cubic bezier and a function to get the point along the bezier at some time t. Despite what you would think from trying to read the literature, this turns out to be trivial -- I mean less than a dozen lines of code.
More thoroughly, explaining away my bulleted list above:
- A spline is a more general term than a "bezier curve": a bezier curve is a particular polynomial function (that I will implement below) that defines a curve that goes from point A to point B given some control points. A bezier spline is an aggregation of n of these. A general spline can be an aggregation of other kinds of curves e.g. a B-spline is composed of a bunch of curves that are generalizations of bezier curves.
- The only kinds of beziers you need to be concerned with are quadratic and cubic beziers. Quadratic beziers are just parabolas and are not interesting. Cubic beziers are curves that go from point A to point B and are tangent to a given line at A and tangent to given line at B. They are defined by A and B plus two other control points that define the tangent lines and the weight that the tangent lines have on the curve.
- Cubic bezier curves are easy to implement. See below.
So here is my curve "library"
Bezier.h
#include class Bezier { private: float x1_, y1_, x2_, y2_, x3_, y3_, x4_, y4_; public: Bezier(float x1, float y1, float x2, float y2, float x3, float y3, float x4, float y4); std::pair getPoint(float t) const;};Bezier.cpp
#include "Bezier.h"Bezier::Bezier(float x1, float y1, float x2, float y2, float x3, float y3, float x4, float y4) : x1_(x1), y1_(y1), x2_(x2), y2_(y2), x3_(x3), y3_(y3), x4_(x4), y4_(y4) {}std::pair Bezier::getPoint(float t) const { float x = (x1_+t*(-x1_*3+t*(3*x1_ - x1_*t))) + t*(3*x2_+t*(-6*x2_ + x2_*3*t)) + t*t*(x3_*3-x3_*3*t) + x4_*t*t*t; float y = (y1_+t*(-y1_*3+t*(3*y1_ - y1_*t))) + t*(3*y2_+t*(-6*y2_ + y2_*3*t)) + t*t*(y3_*3-y3_*3*t) + y4_*t*t*t; return std::pair(x,y);}You define a cubic bezier by making a Bezier object giving the constructor four points. (x1,y1) and (x4,y4) will be the start and end of the curve. The curve will be tangent to line segment (x1,y1)-(x2,y2) at its start and tangent to (x3,y3)-(x4,y4) at the end. To get a point along the curve call getPoint(t) where t=0.0 gives you (x1,y1), t=1.0 gives you (x4,y4), and 0.0 < t < 1.0 gives you the point along the curve in which 100t percent of the curve has been traversed e.g. 0.5 is halfway (in terms of t not arc-length unfortunately).
So that's it. Code is here. I also included a Win32 GDI project that draws cubic beziers, screenshot below. (The sample program is also a little example of how to write a very basic Win32 program, which these days younger programmers seem to appreciate as a sort of parlor trick...)
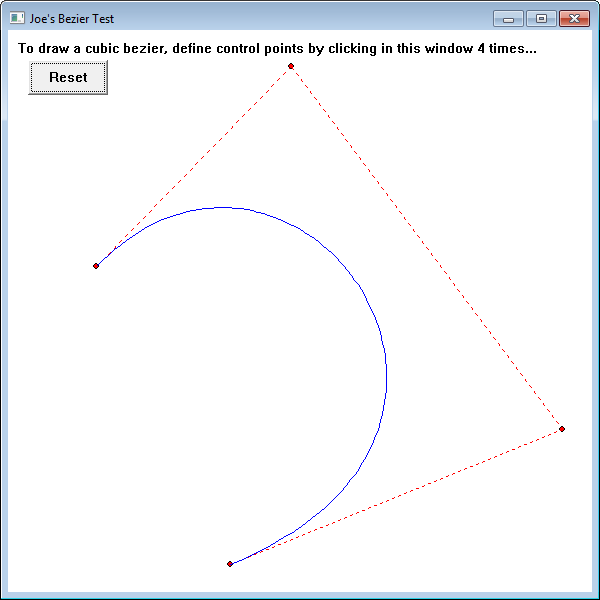
Source


Looks nice :)
A consideration: wouldn't it make more sense as a stand-alone function rather than a class? For that matter, a header file with a single inlined function (perhaps one for each type of curve you support) might make the most sense. Just a thought~!