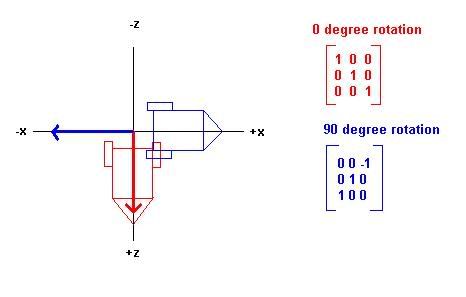
 The diagram view is looking down the y-axis towards -y
An identity matrix (in red) and a 90 degree rotation matrix around the y-axis (in blue) are given, with the resulting position of the model when each is applied.
But the 3rd column of the 90 degree rotation matrix does isn't the correct forward vector. I found that to get the correct foward vector I first have to transpose the rotation matrix. I don't understand why this happens.
When I made a camera class I just took the 3rd column of the orientation matrix and didn't have to bother with transposing it first. I don't understand what is going on.
[Edited by - RunningInt on November 26, 2005 10:30:22 AM]
The diagram view is looking down the y-axis towards -y
An identity matrix (in red) and a 90 degree rotation matrix around the y-axis (in blue) are given, with the resulting position of the model when each is applied.
But the 3rd column of the 90 degree rotation matrix does isn't the correct forward vector. I found that to get the correct foward vector I first have to transpose the rotation matrix. I don't understand why this happens.
When I made a camera class I just took the 3rd column of the orientation matrix and didn't have to bother with transposing it first. I don't understand what is going on.
[Edited by - RunningInt on November 26, 2005 10:30:22 AM]
Matrix Problem
I editted this topic because I realised my problem wasn't with quaternions but with matrices.
I believe the rotation matrix for rotation about the y-axis in right-handed OpenGL is this:
cos (theta) 0 -sin (theta)
0 1 0
sin (theta) 0 cos (theta)
And I also believe you can represent orientation as a matrix. I thought you could take the 3rd column of the matrix to represent the forward vector.
But im having this problem doing that:
 The diagram view is looking down the y-axis towards -y
An identity matrix (in red) and a 90 degree rotation matrix around the y-axis (in blue) are given, with the resulting position of the model when each is applied.
But the 3rd column of the 90 degree rotation matrix does isn't the correct forward vector. I found that to get the correct foward vector I first have to transpose the rotation matrix. I don't understand why this happens.
When I made a camera class I just took the 3rd column of the orientation matrix and didn't have to bother with transposing it first. I don't understand what is going on.
[Edited by - RunningInt on November 26, 2005 10:30:22 AM]
The diagram view is looking down the y-axis towards -y
An identity matrix (in red) and a 90 degree rotation matrix around the y-axis (in blue) are given, with the resulting position of the model when each is applied.
But the 3rd column of the 90 degree rotation matrix does isn't the correct forward vector. I found that to get the correct foward vector I first have to transpose the rotation matrix. I don't understand why this happens.
When I made a camera class I just took the 3rd column of the orientation matrix and didn't have to bother with transposing it first. I don't understand what is going on.
[Edited by - RunningInt on November 26, 2005 10:30:22 AM]
 The diagram view is looking down the y-axis towards -y
An identity matrix (in red) and a 90 degree rotation matrix around the y-axis (in blue) are given, with the resulting position of the model when each is applied.
But the 3rd column of the 90 degree rotation matrix does isn't the correct forward vector. I found that to get the correct foward vector I first have to transpose the rotation matrix. I don't understand why this happens.
When I made a camera class I just took the 3rd column of the orientation matrix and didn't have to bother with transposing it first. I don't understand what is going on.
[Edited by - RunningInt on November 26, 2005 10:30:22 AM]
The diagram view is looking down the y-axis towards -y
An identity matrix (in red) and a 90 degree rotation matrix around the y-axis (in blue) are given, with the resulting position of the model when each is applied.
But the 3rd column of the 90 degree rotation matrix does isn't the correct forward vector. I found that to get the correct foward vector I first have to transpose the rotation matrix. I don't understand why this happens.
When I made a camera class I just took the 3rd column of the orientation matrix and didn't have to bother with transposing it first. I don't understand what is going on.
[Edited by - RunningInt on November 26, 2005 10:30:22 AM]
argh the forward vector is the 3rd ROW of the rotation matrix not the 3rd column.
But that doesn't make any sense. My camera class uses a matrix for orientation and I am taking the 3rd column as the forward vector, and it works.
Does anyone know why in one case you would have to take the 3rd row and in another case the 3rd column?
But that doesn't make any sense. My camera class uses a matrix for orientation and I am taking the 3rd column as the forward vector, and it works.
Does anyone know why in one case you would have to take the 3rd row and in another case the 3rd column?
OpenGL uses a row major format for matrices. Thus each row will correspong to a vector.
Based on your description, it sounds like your camera is using a column major format, which is what D3D uses.
They are basically the same, it's just that the order of multiplications is reversed for the two.
Based on your description, it sounds like your camera is using a column major format, which is what D3D uses.
They are basically the same, it's just that the order of multiplications is reversed for the two.
Quote:OpenGL uses a row major format for matrices.Actually, OpenGL uses column-major format, and...
Quote:...column major format, which is what D3D uses.D3D uses row-major format. So there is some confusion here.
@the OP: My first observation is that your rotation matrix may be the transpose of what it should be. From your example it looks like it may be using row vectors, whereas OpenGL uses column vectors. This may or may not be the cause of your problem, as the only effect of this is to make positive rotation go in the opposite direction.
The other observation is that object and view matrices are different. In the case of OpenGL, in an object matrix the direction vectors are the columns of the matrix, which are the elements (0,1,2), (4,5,6), and (8,9,10). In a view matrix the direction vectors are in the rows of the matrix, which are the elements (0,4,8), (1,5,9), and (2,6,10). Note that we're assuming only rotation and translation are involved; otherwise we'd use the more general term 'basis vector'.
So I'm guessing there are two issues here: getting the original rotation matrix right, and then extracting the direction vectors from the rows or columns as appropriate depending on whether the matrix is an object or view matrix.
To complete jyk's explanation:
One may imagine a virtual camera inside the scene. So the camera may have an object like transformation matrix as any other object. However, the overall transformation one wants to be performed is
object -> world -> view
So the view matrix as is at least applied is in fact the inverse transformation of what the matrix of the camera object contains. As long as only rotation and translation is involved, the inverse of the linear sub-matrix (basis) of such a transformation is simply identical to its transpose. So it comes to the difference of view and object matrices.
So it need not be a mistake, but it is always a question of definition.
One may imagine a virtual camera inside the scene. So the camera may have an object like transformation matrix as any other object. However, the overall transformation one wants to be performed is
object -> world -> view
So the view matrix as is at least applied is in fact the inverse transformation of what the matrix of the camera object contains. As long as only rotation and translation is involved, the inverse of the linear sub-matrix (basis) of such a transformation is simply identical to its transpose. So it comes to the difference of view and object matrices.
So it need not be a mistake, but it is always a question of definition.
This topic is closed to new replies.
Advertisement
Popular Topics
Advertisement




