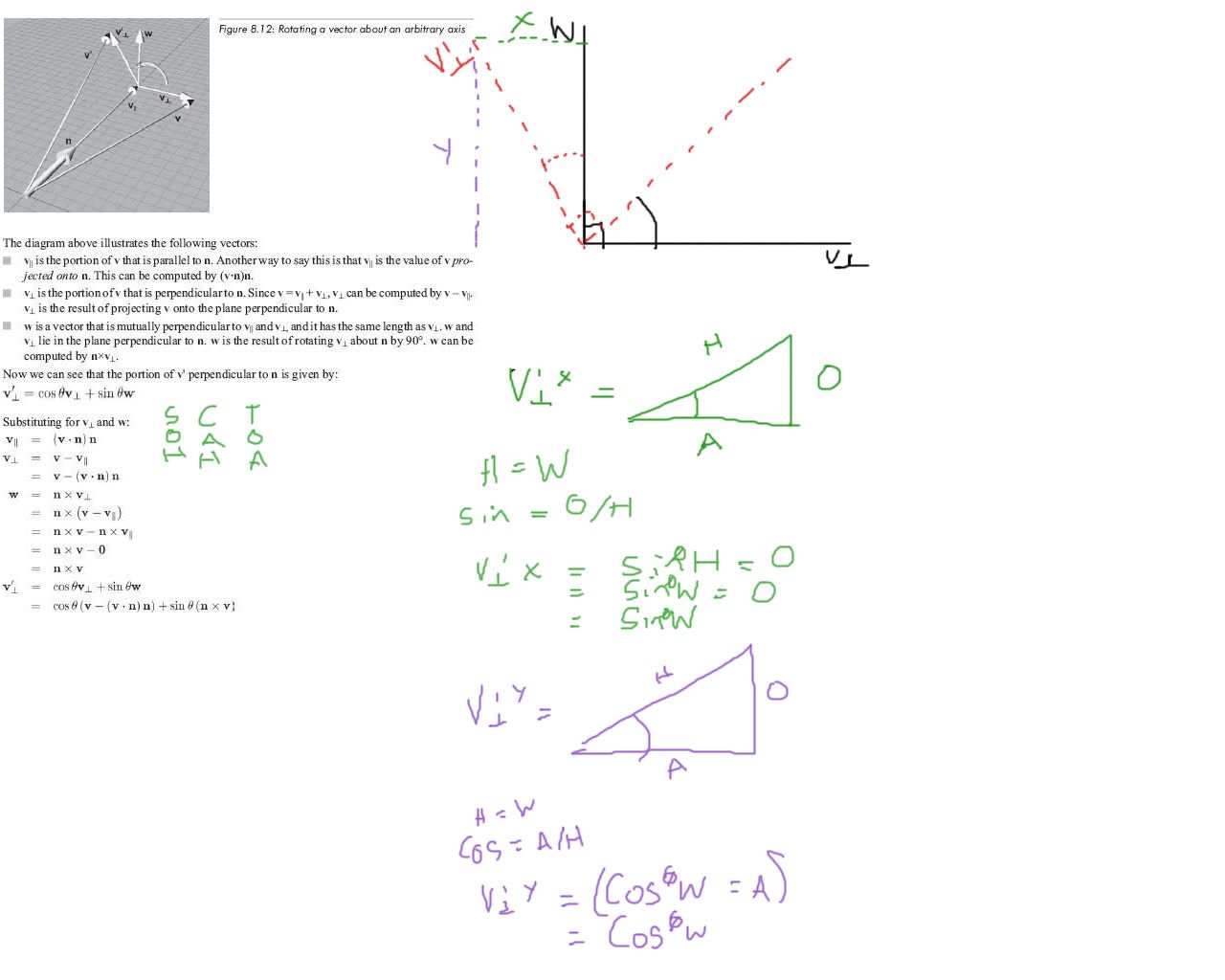
Struggling to understand Arbitary rotation
I really dont understand how the author comes up with that equation, under the sentence " Now we can see ...."
I know that im doing something wrong, but dont know what,
here is my thoughts, can someone point out what im doing wrong?


Think of only one plane in that picture: the one that contains v_perp, w and v'_perp. Think of v_perp and w as forming a basis in that plane. Now you simply want to rotate the point (1,0), which leaves you at (cos(alpha),sin(alpha)). Does that make sense?
Oh yes, that makes sense, the trouble im having is when they introduce the v
ectors, such as
V'T = cos(theta)VT + sin(theta)W
When you say just cos(theta), that makes perfect sense to me, as from my understand its
---->soh, cah, toa
---->cos(theta) = adj/hyp
---->unit circle, so hyp == 1
---->cos(theta) = adj/1
---->cos(theta) * 1 = adj
---->cos(theta) = adj
But when you bring in the vectors such as
cos(theta) * Vec[3] = adj,
i dont understand how they equate to being the hypotenuse, i guess im misunderstanding something here
ectors, such as
V'T = cos(theta)VT + sin(theta)W
When you say just cos(theta), that makes perfect sense to me, as from my understand its
---->soh, cah, toa
---->cos(theta) = adj/hyp
---->unit circle, so hyp == 1
---->cos(theta) = adj/1
---->cos(theta) * 1 = adj
---->cos(theta) = adj
But when you bring in the vectors such as
cos(theta) * Vec[3] = adj,
i dont understand how they equate to being the hypotenuse, i guess im misunderstanding something here
Notice please that the basis mentioned by alvaro defines a co-ordinate system. I.e. v_perp and w define a local co-ordinate system in the world space. The co-ordinates cos(theta) and sin(theta) are then referred to the basis vectors v_perp and w, resp.
Assume you have a local co-ordinate system with a x axis
ex := [1 0 0]
and a y axis
ey := [0 1 0]
Both have unit length. Now you specify a point not by its x,y co-ordinates but by a length and an angle.
p := ( L,theta )
and compute the corresponding reactangular x,y co-ordinates as
px := L * cos( theta )
py := L * sin( theta )
To express this as a vector, you apply the co-ordinates to the belonging axes
p := px * ex + py * ey
== L * cos( theta ) * [1 0 0] + L * sin( theta ) * [0 1 0]
Now, you incorporate the L into the axis vectors, i.e. you scale the co-ordinate system:
== cos( theta ) * [L 0 0] + sin( theta ) * [0 L 0]
Do you see already the similarity to the equation in question?
Now, do the same not in the local co-ordinate space but in the global one. The local [L 0 0] and [0 L 0] vectors have a global equivalent, which can be computed by applying the local-to-global transformation. We don't need to do so explicitely, since they are already computed as v_perp and w. Hence, in global co-ordinates we get
p = cos( theta ) * vperp + sin( theta ) * w
Assume you have a local co-ordinate system with a x axis
ex := [1 0 0]
and a y axis
ey := [0 1 0]
Both have unit length. Now you specify a point not by its x,y co-ordinates but by a length and an angle.
p := ( L,theta )
and compute the corresponding reactangular x,y co-ordinates as
px := L * cos( theta )
py := L * sin( theta )
To express this as a vector, you apply the co-ordinates to the belonging axes
p := px * ex + py * ey
== L * cos( theta ) * [1 0 0] + L * sin( theta ) * [0 1 0]
Now, you incorporate the L into the axis vectors, i.e. you scale the co-ordinate system:
== cos( theta ) * [L 0 0] + sin( theta ) * [0 L 0]
Do you see already the similarity to the equation in question?
Now, do the same not in the local co-ordinate space but in the global one. The local [L 0 0] and [0 L 0] vectors have a global equivalent, which can be computed by applying the local-to-global transformation. We don't need to do so explicitely, since they are already computed as v_perp and w. Hence, in global co-ordinates we get
p = cos( theta ) * vperp + sin( theta ) * w
This topic is closed to new replies.
Advertisement
Popular Topics
Advertisement


