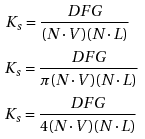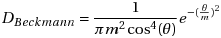I decided to test out Cook-Torrance in place of normalized Blinn-Phong, and while it's not difficult to implement, it's difficult to know if I'm doing it right, mostly because there is some variation depending on what sources you look at. For instance, I've seen three versions for the Cook-Torrance equation:

[attachment=13494:eqn1.png]

I saw PI in the denominator in Cook's paper, I believe I saw nothing in the version in a publication by Wolfgang Engel and in gpwiki.org's D3DBook (probably copied), and on wikipedia there apears a 4, as well as on a video I saw from UC Davis.

Then there is the NDF:

[attachment=13495:eqn2.png]

This is how it apeared in Cook's paper, but I've also seen:

[attachment=13496:eqn3.png]

Someplace I saw that PI was a normilization factor. I'm not sure if this is correct, and if it is why it was not present in Cook's paper or other papers for that matter. I want to be sure that everything is normalized and energy conserving.

Maybe as one last question, I'd like to know the propper way for ensuring that there is energy concervation between specular and diffuse.

Here you go (slide 58)

To ensure energy conservation between specular and diffuse:

fresnelDiffuse = FSchlick(cSpec, light, normal);
fresnelSpecular = FSchlick(cSpec, light, halfway vector);
finalColor = specularColor*fresnelSpecular + diffuseColor*(1-fresnelDiffuse)

You can even approximate the diffuse fresnel (according to tri-Ace):

finalColor = specularColor*fresnelSpecular + diffuseColor*(1-cSpec)

You can use the Schlick Fresnel approximation (in slide 44) to calculate the fresnel.

EDIT: Distinction between diffuse and specular fresnel.

Tiago, that's an approximation, even with the real Fresnel equations, but is not really correct.

Fresnel is dependent on the microfacets oriented towards the halfway vector, but diffuse actually is all the light that is not being reflected, not being absorbed and scattered back out, independent of the microfacets oriented towards the halfway vector. So simply the complement of a single fresnel value won't do it. You would need to solve the integral over all the microfacet orientations with a modified microfacet model:



Your approximation might actually be worse than not having a factor for diffuse at all. If anything I'd use the macro surface normal instead of the halfway vector (just for diffuse though, for specular you should use the microfacet normal):

Tiago, that's an approximation, even with the real Fresnel equations, but is not really correct.

Isn't real-time graphics programming all about approximations?

This is simply the way I've been doing it (that I learned from papers/presentations).

Your approximation might actually be worse than not having a factor for diffuse at all. If anything I'd use the macro surface normal instead of the halfway vector (just for diffuse though, for specular you should use the microfacet normal):

You're right! I just checked my shaders and there's indeed a (1-Fdiffuse) calculated using the macro surface normal and Fspec using the halfway vector).

I just checked a tri-Ace paper and they even approximate the diffuse term like this:

diffuse = (diffuseColor/PI) * (1-f0)
//where f0 is the reflectance at normal incidence

P.S: Could you fix the equations in you're post?

So here is the implementation I'm ussing at the moment:

float3 H = normalize(L + V);
float NdotL = max(0, dot(N, L));
float NdotH = dot(N, H);
float NdotV = dot(N, V);
float VdotH = dot(V, H);

float NdotH_2 = NdotH * NdotH;
float NdotH_4 = NdotH_2 * NdotH_2;
float m_2 = m * m;
float D = exp((NdotH_2 - 1.0) / (NdotH_2 * m_2)) / (PI * m_2 * NdotH_4);

float3 F = R0 + (1.0 - R0) * pow(1.0 - VdotH, 5.0);

float geo_a = (2.0 * NdotH * NdotV) / VdotH;
float geo_b = (2.0 * NdotH * NdotL) / VdotH;
float G = min(1.0, max(0, min(geo_a, geo_b)));

float3 Rs = (D * F * G) / (4 * NdotV * NdotL);
float3 Rd = Cdiff * NdotL;
float3 R = Rs * NdotL + Rd * (1.0 - R0);

Is this correct?

float geo_a = (2.0 * NdotH * NdotV) / VdotH;
float geo_b = (2.0 * NdotH * NdotL) / VdotH;
float G = min(1.0, max(0, min(geo_a, geo_b)));

You can improve this part of the code this way:

float g_min = min(NdotV, NdotL);
float G = saturate(2 * NdotH * g_min / VdotH);

Also, don't ever use max(0, dot(a, b)). Instead use saturate(dot(a, b)) which compiles into a single instruction.

Isn't real-time graphics programming all about approximations?

It is, but is using the complement of Fspecular actually a good one? I don't think so (unless you're using Fdiffuse).

I think someone should approximate a diffuse BRDF using the equation I posted in my post above. That would be a way better approximation.

To get back to the original topic:



The last one is the correct Cook-Torrance microfacet model. Sometimes you find (ns + 2) / (2 * pi) or (ns + 2) / (8 * pi) as the normalization factor for Blinn-Phong. The second one is already pre-multiplied with the 1/4 while the first one is the distribution function for the microfacet model.

And this one is the correct Beckmann NDF:



I wouldn't recommend the Beckmann NDF though. It's pretty damn slow in comparison to other NDFs because of 2 reciprocals and the exponential function. (Y u no use GGX xD)

This is the BRDF I'm using:



I'm using GGX as the distribution function, Schlick's approximation of fresnel as fresnel term and Walter's geometric term for the GGX distribution function.



I color-coded everything for implementation details. The grey parts are just parts of the BRDF and don't need to be implemented. The green parts can be calculated once for every pixel. And the red parts are the only parts, that actually need to be calculated for every light.

I've approximated the diffuse transmittance integral and created a BRDF which is pretty lightweight but also pretty physically accurate. Use this instead of Lambert if you want to have proper energy conservation. It's based on GGX roughness though, so you might need to convert your roughness to GGX roughness:

It's actually just a single MAD instruction per light if you implement it, the rest can be done on a per pixel basis.

Ok, so I've been giving GGX a look. Unfortunately I haven't been able to find much information on it, at least not nearly as much as Beckmann's.

I gather this is the correct normalized version?

[attachment=13573:eqn.png]

Currently I've only evaluated the Blinn-Phong NDF, Beckmann and what I think is the correct GGX NDF. One thing that I noticed right away is that Blinn-Phong and Beckmann are nearly identical for roughness values below 0.3 or so. From 0.3 to 0.5 they are still pretty similar. GGX on the other hand is substantially different across the board, and that was with the Cook-Torrance G function. Next I tried your BRDF and the differences grew even further. I'm not sure which is more physically correct, but to my eyes I think I might prefer Beckmann + Cook-Torrance.

Here is a graph of theta H for a roughness of about 1.2:

[attachment=13574:Untitled.png]

Blue is Beckmann and C-T G. Red is GGX and C-T G. Green is your BRDF.

The only difference between mine and your GGX, is that I'm using the Walter GGX geometric term which is specifically calculated using Smith's "blackbox" function to convert any distribution function into a perfectly matching geometric term. The thing is, that the cook torrance geometric term is more or less completely absurd and unrealistic, because the shadowing and masking should be dependent on the microfacet distribution, but the cook torrance geometric term completely ignores that. That's why you get that unrealistic cut at 45 degrees. I'd recommend you take a look at Naty Hoffmann's presentation and Disney's presentation at http://blog.selfshadow.com/publications/s2012-shading-course/. You should also check out Disney's BRDF Explorer and the MERL database. With the BRDF explorer, you can validate how well your BRDF matches actual materials from the MERL database.

Also, your GGX is the correctly normalized version ;)