Hi,
I've managed to implement a reasonally flexible lighting shader, including both directional and point lights. With various numbers of max. lights (different copies of the effect/shader).
But there's something strange with the light attenuation of my point lights.
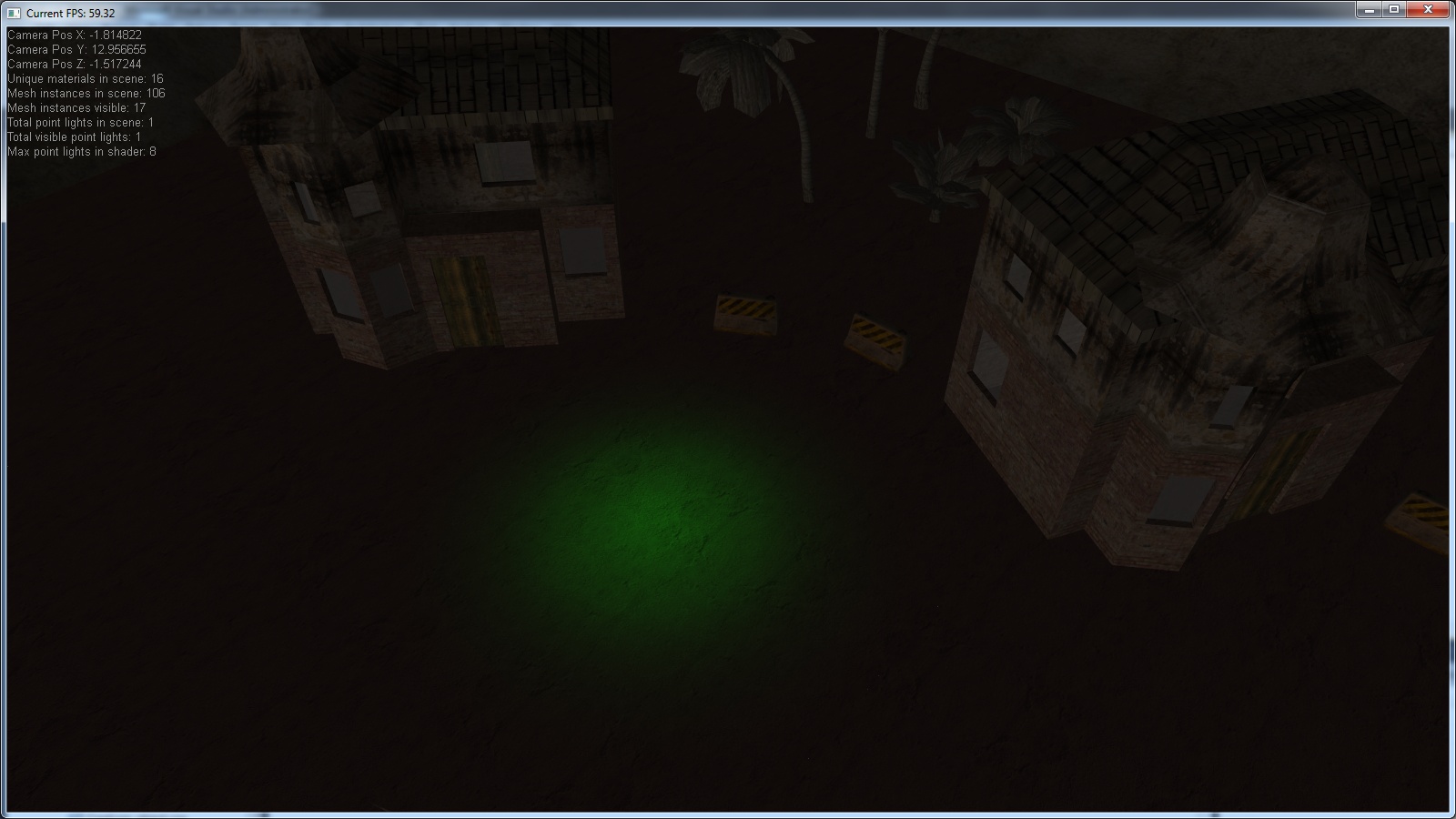
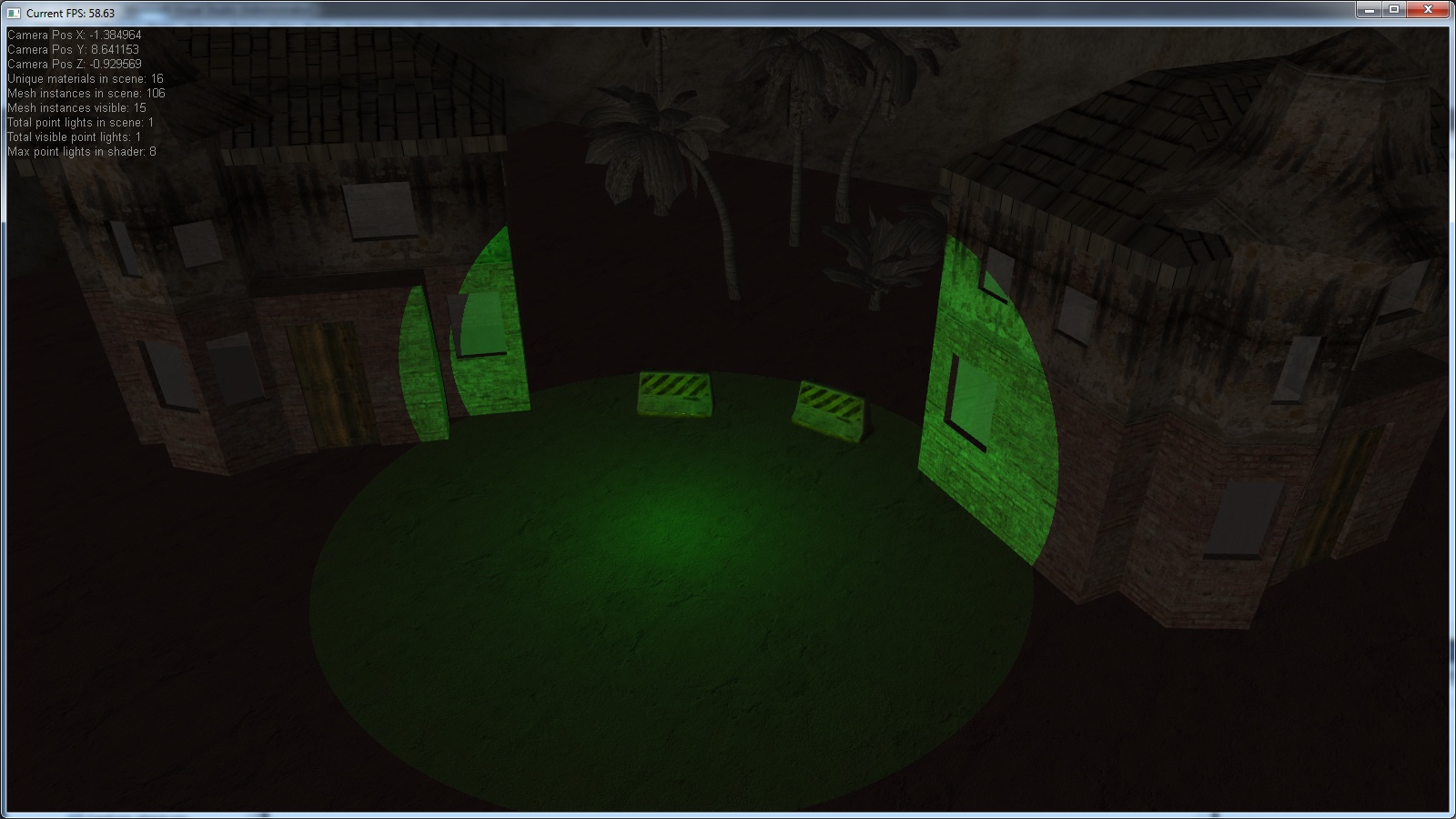
For testing purposes I've set up the following scene:
- place a point light at position x (-5, 1, 5)
- give the point light a max. range of 5.0, fullpower (full bright) range of 3.0
- place a sphere with blended material at position x (-5, 1, 5)
And then simply check if the point light stops shining where the sphere begins.
Unfortunately... it doesn't.
I've double checked the range/scale of the sphere, it matches the 5 'units' in the same scale as the pointlight range of '5'.
Here's a screenshot of the result and the actual attenuation calculation.
Any idea where it's going wrong?

// PER PIXEL ATTENUATION
float dist = length(PointLightPos[i] - input.wPos);
float att = saturate(1 - (dist - PointLightFPRange[0]) / (PointLightRange[0] - PointLightFPRange[0]));
att *= att;