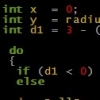
... can you maybe say me how to clip that?
With 2 points p1, p2 giving a straight line segment, a ray can be formulated so that the ray's independent parameter, t, restricts the ray to have only points on the said segment:
r( t ) := p1 + t * ( p2 - p1 ) w/ 0 <= t <= 1
When both points are given in camera space then the ray is given in camera space, too. With n being the distance of the near clipping plane along z, we can first check whether both points (and hence the entire line segment) would be culled
p1z < n AND p2z < n then culled
or else both are inside the view volume
p1z >= n AND p2z >= n then project into 2D as is
or else clipping is needed (i.e. one point is on this and the other point is on the other side of the plane).
If clipping is needed, then the segment intersects the clipping plane. The plane has z = n everywhere, so the intersection point must have z = n, too. The z co-ordinate of the ray should hence be
rz( tn ) = p1z + tn * ( p2z - p1z ) == n
Solving this for tn can be done analytically
tn = ( n - p1z ) / ( p2z - p1z )
and be computed numerically as long as p2z - p1z is not zero (if it is zero then the line segment lies totally inside the clipping plane and can be used as is). Computing the ray's x and y co-ordinates with the found tn gives you the other both co-ordinates of the intersection point.
r( tn )
So replace those one point p1, p2 that has its z less than n with r(tn), and continue as usual.