I would like represent my object as mass spring mesh to simulate soft body dynamics.
Mass represent vertex while edge represent spring that connect two adjacent vertex.
I
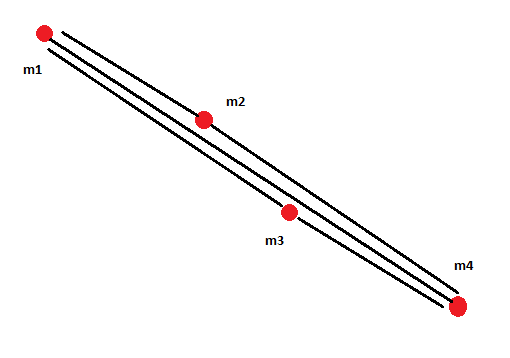
I draw a this simple example to explain my problem.
I have four mass m1,m2,m3,m4 and know the values and their positions.
I know the stiffness coefficient kij and dumping coefficient cij of mesh springs where i and j are the vertex index.
In figure 1 the system is in the rest position.
In figure 2 after apply a force to m4 point the system change configuration,
The user move the m4 point from figure 1 to figure 2 position.
A force applied to m4 move the mass m4.
m1 mass rest in the same position again in figure 2 while mass m2 e m3 have a new position.
I would like calculate the new position of m2 and m3 mass after that user move the m4 mass.
I know the formula about Fi_int the internal force on the vertex i and the damping force Fi_ext on the vertex.
Please help me solve this problem.