Prior to that I had taught myself a large amount of Trigonometry, so mainly these days I only struggle with Calculus, which is mostly a mystery to me.
I am looking at this example code here:
http://math60082.blogspot.jp/2013/02/question-write-function-to-calculate-nx.html
I get that integration is just the sum of the values from the start to the end in slices, each slice put through whatever equation is right of the integration bar, but I could never write the code to do that on my own, at least not in this example. Here are example of things that confound me:
His first lines of code are:
// add in the first few terms
sum = sum + sin(a) + 4.*sin(a+h);
// and the last one
sum = sum + sin(b);Then there is h. What is this magical number?
I can see from his code:
h=(b-a)/N;After this my head just explodes.
I’m assuming his first pass with the sin() calls is basically part of a hemispherical integration template (when integrating over a hemisphere/curve, this is just how you do it) meant to test that he is integrating over an arbitrary circle correctly, but then he changes to exp() and by this point I just give up trying to follow how he took the formula and made the code.
I don’t see where he actually did the math in the formula, and instead at the end he pulled an atan() and sqrt() out of his ass and it’s all good.
So I would like 2 things:
#1: A break-down of this particular formula and conversion so I can have a good set of formulas whose conversions into code I can at least follow.
#B: I somewhat want to be spoon-fed on this particular example, but I definitely want to be able to do all of these on my own easily. I am so tired of not being able to follow equations in research papers and even worse unable to make my own. I want to know some good places, even if not free, online, where I can go through a course at a reasonable pace for a working person with 20 dates with supermodels every week.
A place that is structured like a high school class, possibly even with homework, but with the important point being that it teaches the information from start to finish step-by-step.
L. Spiro





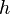 is the "step length", given by
is the "step length", given by  - see
- see 






