What algorithm should I use to find the minimum flow of a digraph where the flow across each edge has an infinite upper bound but a non-zero lower bound?

Like this for example:

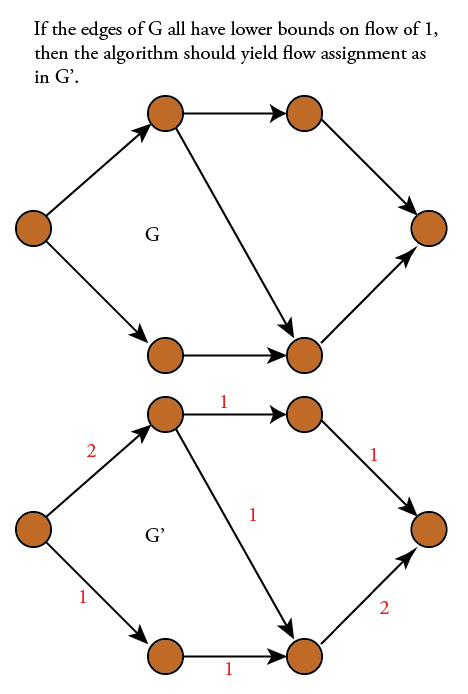
In the literature this is a minimum cost flow problem. In my case however the cost is the same as a nonzero lower bound on the flow required on each edge so I worded the question as above. In the literature the question would be: what is the best algorithm for finding the minimum cost flow of a single-source/single-sink directed acyclic graph in which each edge has infinite capacity, a non-zero lower bound on flow, and a cost equal to the lower bound on flow.

From my research it seems that the main way people deal with any kind of minimum cost of any kind of network is to set the problem up as a LP problem and solve that way. My intuition, however, is that not having upper bounds on flow ,i.e. having edges with infinite capacites, makes the problem easier, so I was wondering if there is an algorithm specifically targeting this case using more "graphy" techniques than the simplex method et. al.

Do you need to find the flows for every edge, or only the minimum flow for the entire graph? (EX: Your example graph has a minimum of 3... if I'm understanding terminology anyway). There may be some kind of simpler method based on observations about the graph if you don't actually need to find the flow at every edge.

You need to find a flow that meets the lower bound for the edge for each edge so if each edge has a lower bound > 0 then each needs to have flow running through it. You also want flow rules to be obeyed and for total flow to be a minimum.

If you start out by setting the flow across each edge to the lower bound then flow rules will not necessarily be obeyed. For each vertex, you can then calculate the difference between the in-flow and the out-flow, call this number D(V). Then you need to deal with the vetices that have non-zero D(V). For a vertex, v that has negative D(v) you need to augment the flow from the source to v. For a vertex with positive v, you would need to augment the flow from v to the sink. You could do this just by finding a shortest path in both cases and augmenting along the shortest path, but I have no idea if doing this would result in the global minimum.

Also seems like it might be inefficient -- not sure. in the toy case above, assigning the lower bounds as the flow is a decent approximation of the minimum flow but that is because this is a toy example -- imagine there are dozens of vertices or hundreds of vertices with arbitrary lower bounds. For my use case, there will probably be at most something like 60 or 70 edges with 30 more likely but this calculation would need to be performed during every iteration of the game loop (this would be for version 2 of my puzzle game Mondrian which I want to develop for the iPad -- but want to change the fundamental algorithm to what it always should have been)

I think I have a solution: Find a [non-minimal] valid configuration (something with D(v)=0 for all v), then try to compute how much you can reduce the flow through each pipe. Since you have a lower bound for the flow through each pipe, the numbers you are trying to compute have maximum values. But these numbers also need to satisfy a condition like D(v)=0, so we have reduced the problem to a maximum-flow problem and we can use the Ford-Fulkerson algorithm.

I don't think you can do better than that.

Yes, this is good ... now I just need a way of finding a feasible flow in a single traversal.

EDIT: Yeah, so I think it can be solved as two max flow problems. The in-flow(v) - out-flow(v) function that I was calling D(v) above can be viewed as node supplies and demands which you can figure out how to satisfy via a max flow problem. you can construct a graph from the original graph as explained here: (where x(v) is what we were calling D(v))

such that if you find max flow of the new graph, the flow on the edges in this max flow plus the lowerbounds on the original graph will be an admissible flow on the original graph which you can then minimize with another max flow problem as alvaro explained above.

Computing a feasible flow doesn't seem terribly complicated. For each edge on the graph you can find a path that contains it. Then start with 0 flow for every edge, loop over the edges and add the minimum flow for the each edge to the path that includes this edge. I am not sure if this can be done in "single traversal", because it's late and because it depends on exactly you mean by that. But I think it will be faster than solving another max-flow problem (although I didn't fully follow what you posted).

See, I was thinking that finding a feasible flow like this has really bad running time but I think it doesn't at least not relative to max flow. You could just do a complete depth-first traversal and then when you either reach t or reach an already-discovered vertex augment the current path you are on with the max lowerbound of the set of edges that were newly discovered on the current path, going all the way to t each time you do this. This would have running time of something like O(E * Avg. length of paths from s to t).

The algorithm involving two max flows is what you need to do when edges have both lower bounds and upper bounds, as someone is discussing in this power point file.

There also turns out to be a small amount of literature on this problem itself -- that is, minimum flow -- not just as a use of max flow or as formulated as minimum cost: see here and here, for example, but all of this material deals with the case in which there are lower and upper bounds. It actually surprises me that there is nothing in the literature about the no upper bound case; it seems like a very practical problem.