With the revolution of consumer 3D graphics cards, there was a boom in 3D games. Most of these were first person shooters, and for a very good reason. The reason is that indoor environments, when compared to outdoor environments, are far simpler. With the great outdoors, there are no convenient staircases to the next level, or doors and walls blocking your view. Believable outdoor environments go on for miles. The sheer geometry involved is phenomenal, and any steps to cut this down are welcomed. Enter quadtrees.
Note: the following diagrams are a top-down view of a 3D terrain. The grid shows the terrain on the x/z axis, as the actual "height" (i.e. hills) isn't visible, as we are looking down the y-axis.
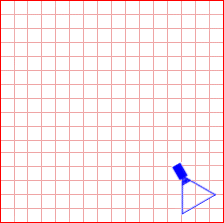
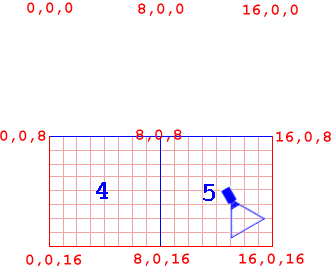
Imagine your terrain as a large grid, extending in the x/z plane. Take a look at Figure 1. Here, we have the camera located in the bottom right of the terrain, with the viewing frustum (the blue triangle) extending a few cells in the same direction. So, before any optimisations, the routine for drawing the terrain would look like this:
for(int ctr=0; ctr
{
DrawCell();
}(Note: a cell is just a square containing a number of triangles that are part of the terrain.) This is all very nice, but as our terrain is 16x16 cells, 256 cells are being drawn. This is a lot of wastage, as only 5 cells are in our viewing frustum! Now our first optimisation: we'll test each cell to see if it lies in our viewing frustum, and if it does, draw it. Now our code looks a little like this:
for(int ctr=0; ctr
{
if(cell is in frustum) DrawCell();
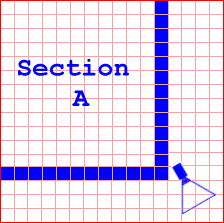
}If the cell is in our frustum, we'll draw it. Right, now we're only drawing 5 cells, as opposed to 256. With that bit of modified code, we've saved ourselves drawing 251 cells! But, once again, it is very inefficient. Take a look at Figure 2.
I've shaded certain cells blue, so they create a bounding box. If the blue cells aren't in the frustum, then we can safely say that the cells inside Section A won't be either. If we know that the blue cells aren't in the frustum, why do we bother testing the other 144 cells in section A? That's were quadtrees come into play.
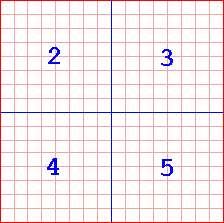
Quadtrees take the terrain, and divide it up it into four smaller parts, then those smaller parts into four smaller parts, and so on, until it reaches a set size. That may seem a little confusing, but let me explain with pictures. First, we start off with our grid. We now divide that grid into 4 smaller sections.
As you can see from Figure 3, we now have four subsections of our terrain. We now need to keep dividing into 4 sections, until we reach, say, a section of only 1 cell. So, in our next diagram, we'll divide the first section into four smaller parts.
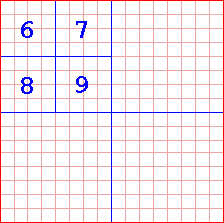
Again, we'll divide one section into 4 smaller parts:
And again, we'll divide a section into four more parts:
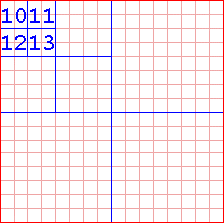
Ok. We've divided our section again, and its sub-sections are only one cell wide and tall. We tell our tree to stop dividing this section, but carry on to the next. Eventually, the whole tree will be divided up. So, to recap, to create a quadtree, you divide it into four sections, then those sections into four sections, then divide those smaller sections into four sections, and so on. When do we stop? When we reach a certain size. This size is abitary, so make it up yourself. In our example, we'll say each cell contains 16 triangles (4x4), so we'll stop when our subdivisions are one cell by one cell. We could keep on going, but we wont. One thing I haven't told you is the parent/child relationship. Each subdivision (called a Node) has one parent (the Node, which it was split from,) and four children. The exceptions are leaves, which only have a parent. A leaf is the smallest subdivision we allow, in our case, one cell by one cell. Another thing: before you subdivide, you have a root: The root has no parent, but, like the rules, has four children. Still don't get it? Let's have an example. You know those susceptible chain letters? It's like that. One person (the Root) sends a letter to four people (the Root's children). Now, these four people (Nodes) share the same parent: the evil conspirator (the Root). The letter says "Send this letter to four more people else you'll have seven years bad luck/unlimited fame/whatever." So, each one of those four people send the letter to four more people, and so on.
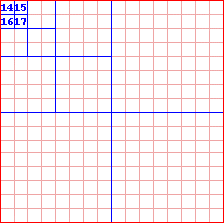
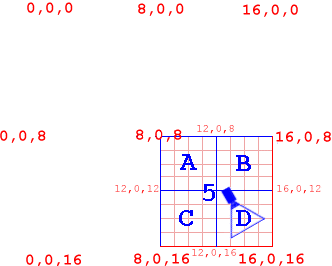
Look at figure one again. The dark red border is the root. In Figure 3, we divide the root, and assign it its children. The four squares represented by the blue line are the roots children. We'll call them Node 2, 3, 4 and 5 respectively. In Figure 4, we took the first child of the root (node 2), and divided it up into 4 more squares. These squares are that node's children. All of those children share the same parent: The first child of the root, or, as we called it, node 2. We'll call these nodes Node 6, 7, 8 and 9. Once again, we divide node 2's children into four more squares (nodes), and we'll name these 10, 11, 12 and 13. Nodes 10-13's parent is node 6. This is represented in Figure 5. In Figure 6, we divide node 10, giving us leaves 14, 15, 16 and 17. As they are leaves, we don't divide them, go back and carry on dividing our next node, node 11. When node 11 is done, we do 12 then 13, then 7, 8 and 9, then 3,4 and 5. Then we're done.
I know that's a really jagged piece of toast to swallow, but read it carefully. Then again. If you're still unsure, have a gander round the web. You'll probably click eventually, as they are easy to understand if explained correctly. In a final desperate attempt, I'll walk you through the process of using a quadtree. But first, let's have a nice summary:
A quadtree divides terrain into four pieces, and divides those pieces into four pieces, and so on, until it reaches a certain size, and stops dividing.
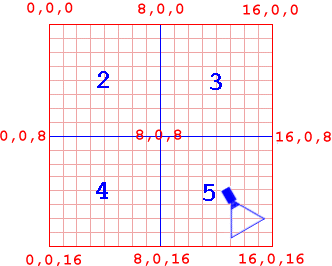
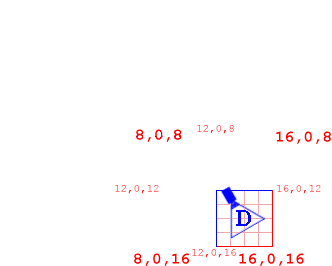
Quadtrees work by using the bounding coordinates of a node. Let's say our map goes from 0 - 16 in the x-axis and 0 - 16 in the z-axis. In that case, the bounding coordinates of our whole map are top-left = (0,0,0), top-right = (16,0,0), bottom-left = (16,0,0), and bottom right = (16,0,16). When we split the root node, we split its bounding coordinates as well, so node 2 has bounding coordinates: top-left = (0,0,0), top-right = (8,0,0), bottom-left = (0,0,8), and bottom right = (8,0,8), as in Figure 7.
[size="3"]Test 1
The way it works is we start at the root and say "Is the camera within the root's bounding coordinates?". Unless something is wrong, we say "yes". We know the camera is within the root's children, so now we test them. "Is the camera within Node 2's bounding coordinates?". The answer here is no, so we can dismiss node 2 and all its children. So far, we have dismissed testing 64 cells (the number of leaves in Node 2). Not bad, not bad.
[size="3"]Test 2
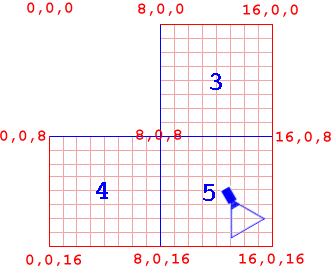
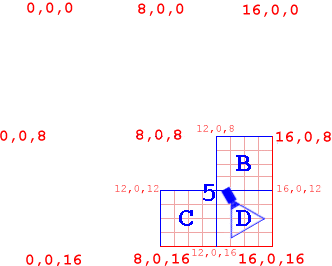
As you can see in Figure 8, I've removed Node 2 and all its children for the sake of clarity. Once again, we test the tree. "Is the camera within Node 3's bounding coordinates?". Again, the answer is "no", so we can safely dismiss Node 3 and all its children.
[size="3"]Test 3
So, here we go. "Is camera within Node 4's bounding coordinates?". No surprise, the answer is "no". Time to test Node 5.
[size="3"]Test 4
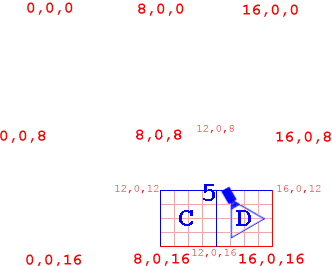
This time, the camera is within Node 5's bounding coordinates, so we test its children. I've named Node 5's four children A, B, C and D for clarity. Time to test Node 5's first child. "Is camera within Node A's bounding coordinates?". Looking at Figure 10, we can see that it isn't, so we'll dismiss Node A and its children.
[size="3"]Test 5
Now let's test Node 5's second child. "Is camera within Node B's bounding coordinates?". Looking at figure 11, we can see that it doesn't, so we'll dismiss Node B and its children.
[size="3"]Test 6
Right, let's test Node C, Node 5's third child. "Is the camera within Node C's bounding coordinates?". 'Course it's not, so let's just rid ourselves of node C altogether.
[size="3"]Test 7
Ok, it has to be in Node D. "Is the camera within Node D's bounding coordinates?" "Yes, yes it is." Finally. Now all we have to do is test all of Node D's children (groan). Well, I'm gonna stop here. Think of working the rest out as an exercise
A quadtree is used to dismiss large chunks of terrain at a time. If an apple is on a tree's leaf, chopping off the branches the apple is nowhere near saves you looking on every leaf.
[size="5"]Putting it Together: Coding a Quadtree
Before we go any further, I advise those who are unsure about Indexed Lists to read through my tutorial here.
So, now we've got the theory under our belt. How do we put it together? We will need:
- A structure to hold our Quadtree data
- A function to create the tree
- A structure to hold triangle data
typedef struct node
{
int bType;
VERTEX vBoundingCoordinates[4];
unsigned int uiBranches[4];
unsigned int uiVertexStrip1[8];
unsigned int uiVertexStrip2[8];
unsigned int uiVertexStrip3[8];
unsigned int uiVertexStrip4[8];
unsigned int uiID;
unsigned int uiParentID;
}NODE;The variable bType tells us what type this node is. It can either be NODE_TYPE or LEAF_TYPE. If we are drawing our tree (terrain), it is used as a flag to tell the program to either stop and draw some triangles (LEAF_TYPE) or carry on reading through the tree (NODE_TYPE).
Next is an array of 4 vertices. These hold the node's bounding coordinates. The layout for the structure VERTEX is as follows:
typedef struct vertex
{
float x,y,z;
}VERTEX;Now we have an array called uiBranches. This is an array of four indexes to the quadtree array. These indexes are the 'children' of the node. If the bType is LEAF_TYPE, this isn't used.
As we said each leaf would hold 16 triangles, we have 4 arrays, named uiVertexStrip1 to uiVertexStrip 4. Each of these arrays holds 4 indexed triangles in the form of a triangle strip. In this tutorial, we won't be using these, so we won't go into detail about them (it also saves me an explanation).
The variable uiID holds the nodes ID in the quadtree. As I said before, the quadtree is just an array of nodes. The ID is just an index in that array.
Then we have our last variable, the uiParentID. This is the ID (index) of the parent. This, coupled with the uiBranches array, lets us navigate our way round the tree, by jumping from node to node. At any given node, we can go to its parent or its children, which, if we follow the tree, will take us to the root, or all of the leaves.
NODE *pNodeList;The line above creates a pointer structure called pNodeList. It can be called anything. Basically, it is our quadtree. Note: we'll use array element pNodeList[0] as our root.The above formula gives us the number of leaves. The Leaf Width is the number of triangles across in each leaf. As we said each leaf will be one cell by one cell, we also said each cell contains 16 triangles. In our case, seeing as cells are 16x16 triangles, the Leaf Width will be 4. Grid Width is the width of the grid in triangles. As each cell is 4 triangles across, 16 cells x 4 is 64. To find out the total number of nodes in the tree, we call the function CalcNodeNum. Below is the function CalcNodeNum:
unsigned int CalcNodeNum(unsigned int max,unsigned int min)
{
int ctr=0;
int var = 0;
while(var==0)
{
ctr+=max;
max=max/min;
if(max==1)
{var=1;}
}
ctr++;
return ctr;
}Here, CalcNodeNum takes two parameters: the total number of leaves (max), and the leaf width (min). In our case, the leaf width is 4 triangles. The total number of leaves was obtained in the previous formula. What CalcNodeNum does is keep on dividing the grid by min to get the total number of leaves. Step through the function to understand it better. So, let's get the next bit of code done:
unsigned int Temp =(GridWidth/4)*(GridWidth/4);
unsigned int Temp2 = CalcNodeNum(Temp,4);
pNodeList = (NODE*)malloc(sizeof(NODE)*Temp2);Ok. The first line uses Formula 1 to calculate the total number of leaves. The second line stores the total number of nodes in an unsigned integer called Temp2. The third line allocates memory for pNodeList. We typecast the function "malloc" with our structure "NODE". Then, we allocate memory for Temp2 nodes by multiplying the number of nodes by the size of the NODE structure. For more information, check out the "malloc" and "sizeof" functions in your compiler's help file. Now that we've calculated the number of nodes and allocated memory for our quadtree, let's call our quadtree creation function.
But first, let's lay the foundation knowledge for recursive code. We'll use a number counter as an example. If we want to display the numbers 1 to 10, we could do this:
void Count(int num)
{
cout<
}
void main()
{
Count(0);
Count(1);
Count(2);
Count(3);
Count(4);
Count(5);
Count(6);
Count(7);
Count(8);
Count(9);
return;
}But as you know, that would be tedious every time we wanted to count with numbers. So, the natural progression would be something like so:
for(int ctr=0;ctr<10;ctr++)
{
Count(ctr);
}Although there is nothing wrong with the above code, using it for our quad-tree would be a real nightmare. This would involve having lots of temporary values and it would take a lot of time to get right. You'll understand why once we've coded our quadtree. In the above code, we have actually implicitly called Count 10 times ourselves. If we wanted to call it 20 times, we would have to explicitly tell the 'for' statement 20 times. Recursive code needs only be called once. There is no need for 'for' or 'while' statements. The reason is that we call the recursive function, and it calls itself however many times we tell it to. So, to the code:
void Count(int num)
{
static int ctr = 0;
if(ctr>num)
{return;}
else
{
cout<
ctr++;
Count(num);
}
}
void main()
{
Count(ctr);
return;
}The static integer 'ctr' means that 'ctr' is declared once (the first time the function is called), but its value is used by subsequent calls to the function. It is like a global variable which only Count can see. As you can see, we only call Count once. It keeps on calling itself until a certain condition is met (in our case, when 'ctr' reaches the value of 'num'). So, when we, the programmer, call Count for the first time, we have to set it up. We give it a condition to meet, in our case the number 10. If we wanted it to count to 20, we would pass '20' to Count when we call it. Right, let's summarise that:
The programmer only calls a recursive function once. The first call (made by the programmer) tends to 'initialise' the function, telling it what to do and what conditions are needed to stop calling itself.
Well, I'm glad that's out the way. On with our code. Now, let's look at the function CreateNode. As the name suggests, this creates nodes. If only it were that simple
void CreateNode(unsigned int Bounding[4],unsigned int ParentID,
unsigned int NodeID)This function returns nothing. Nil. Void. If you want, you could make it return something like a BOOL for error checking, but for this tutorial, I know the code works, so we'll leave it as 'void'
In a 2D array extending in the x/z plane with height values of '0' (i.e. our grid), to find the top left, we use the following equation:
Wow, that'll get your head scratching. Don't get too cocky, as that was the easy bit. To find the top-right, we use the following equation:
Easy, easy... Now let's try the bottom-left:
And now the bottom-right:
The mathematics isn't hard, but if you're having trouble understanding it, then just plot a grid on some paper (or better yet, squared paper), and step through it. Now we're ready to call CreateNode:
unsigned int uiBoundingCoordinates[] =
{0,GridWidth,(GridHeight*(GridWidth+1)),
((GridHeight)*(GridWidth+1))+GridWidth};
CreateNode(uiBoundingCoordinates,0,0);What we have done is set up the root node. The root node has the bounding box described above, no parent (so a parent ID of 0), and its ID is 0, i.e. the first element in our quadtree array. We are now prepared to walk through the CreateNode code.
void CreateNode(unsigned int Bounding[4],unsigned int ParentID,
unsigned int NodeID)
{
static unsigned int TotalTreeID = 0;
unsigned int uiNodeType;
unsigned int uiWidth,uiHeight;Ok, the static unsigned int 'TotalTreeID' holds the current number of nodes. We use this later on to assign the nodes children their IDs. The unsigned int uiNodeType holds the node's type, either a leaf (LEAF_TYPE) or a node (NODE_TYPE). The unsigned ints uiWidth and uiHeight will hold the width and height of the node. As we are passed just bounding coordinates, we don't actually know the dimensions of the node. We use the uiWidth and uiHeight to tell whether the node is a leaf or node. Now we need to get the width and height from the bounding coordinates:
uiWidth = fVerts[(Bounding[1]*3)] - fVerts[(Bounding[0]*3)];
uiHeight = fVerts[(Bounding[2]*3)+2] - fVerts[(Bounding[0]*3)+2];This assumes fVerts is an array containing a list of vertices, which build up our grid. As a vertex contains 3 parts, x, y and z, each vertex in the array will occupy 3 elements. Normally, if we have an index of value 3, it would point to the third element. But... as each vertex occupies 3 elements, and index of 3 would point to the third element, i.e. Vertex 0's Z component.
As you can see, an index of 0 points to element[0]. Element [0] is Vertex 0's X component. Element 3 is Vertex 1's X component. This is all very nice, but our indices are wrong, right? Surely if Bounding[0] was '3', it wouldn't point to the third vertex, but the second vertex's X component? Well, we multiply the index by 3 for the vertex's X component, add 1 for the Y component, and add one more for the Z component. so, if we have an index of 3, it's supposed to point to vertex 3. Ok, 3*3 is 9, and the ninth element is vertex 3's x component. So, if we wanted index 3's z component, we would do (3*3)+2, which gives us element 11, vertex 3's Z component! To find the width of the node, we subtract the top-left vertex's X component (remember, x values in our grid go across, so they represent width) from the top-right vertex's X component. And to find the height, we subtract the top-left vertex's Z component (when we say 'height', we mean the depth, but we call it 'height' to make it easier to picture as a 2D grid) from the bottom-left vertex's Z component.
Now, we said that our leaves are 4x4 triangles. This implies that leaves are 4 triangles wide. As we know the width of the node (stored in uiWidth), if we divide the width by 2 and get a result of 2, then the width is 4, and hence our node is a leaf.
if(0.5*uiWidth==2)
{
uiNodeType = LEAF_TYPE;
}
else
{
uiNodeType = NODE_TYPE;
}Notice that multiplying by 0.5 is the same as dividing by two. Next, we want a pointer to our node. The reason for this is to save me getting RSI from typing the same thing about 50 times. So, pNodeList contains all our nodes, we just need to select our node:
NODE *pNode = &pNodeList[NodeID];All this means is that instead of doing stuff with our node like so:
pNodeList[NodeID].uID = Whatever;We can simply do this: pNode->uiID = Whatever;The next bit just fills our node with values we have already discussed. pNode->uiID = NodeID;
pNode->uiParentID = ParentID;
pNode->vBoundingCoordinates[0].x = fVerts[(Bounding[0]*3)];
pNode->vBoundingCoordinates[0].y = fVerts[(Bounding[0]*3)+1];
pNode->vBoundingCoordinates[0].z = fVerts[(Bounding[0]*3)+2];
pNode->vBoundingCoordinates[1].x = fVerts[(Bounding[1]*3)];
pNode->vBoundingCoordinates[1].y = fVerts[(Bounding[1]*3)+1];
pNode->vBoundingCoordinates[1].z = fVerts[(Bounding[1]*3)+2];
pNode->vBoundingCoordinates[2].x = fVerts[(Bounding[2]*3)];
pNode->vBoundingCoordinates[2].y = fVerts[(Bounding[2]*3)+1];
pNode->vBoundingCoordinates[2].z = fVerts[(Bounding[2]*3)+2];
pNode->vBoundingCoordinates[3].x = fVerts[(Bounding[3]*3)];
pNode->vBoundingCoordinates[3].y = fVerts[(Bounding[3]*3)+1];
pNode->vBoundingCoordinates[3].z = fVerts[(Bounding[3]*3)+2];
pNode->bType = uiNodeType;Now, in this tutorial I won't deal with leaf nodes. Once we've assigned a leaf node its type (LEAF_TYPE), I'm going to just return to the calling function (i.e. do nothing). In the real world, you may wish to have a leaf point to an array or triangles. If you have a look at the NODE structure, you'll notice I left 4 vertex strips (uiVertexStrip1...4), which, if you want, you can fill with triangles. This is so when you are drawing the terrain and you hit a leaf, you can tell it to draw those triangle strips (which represent that portion of the terrain).
if(uiNodeType == LEAF_TYPE)
{
return;
}
else
{Next, we need to do the following for each of the node's children: Add one to uiTotalTreeID, create a new bounding volume for that child, call CreateNode passing the new bounding volume, NodeID for the parent ID and uiTotalTreeID for the new node's (child's) ID.
unsigned int BoundingBox[4];
TotalTreeID++;
pNode->uiBranches[0] = TotalTreeID;
//Top-Left i.e. b[0]
BoundingBox[0] = Bounding[0];
//Between b[0] and b[1]
BoundingBox[1] = Bounding[0]+((Bounding[1]-Bounding[0])/2);
//[between b[0] and b[2]
BoundingBox[2] = Bounding[0]+((Bounding[2]-Bounding[0])/2);
//middle of node
BoundingBox[3] = Bounding[0]+((Bounding[2]-Bounding[0])/2)+
((Bounding[1]-Bounding[0])/2);
CreateNode(BoundingBox,NodeID,TotalTreeID);What we have done is split the bounding volume to 1/4 its size. We do this differently for each child, as the above shows splitting for the top-left child. Notice for the top-left of the child, it is the same as the top-left of our node. The top-right of the child will be halfway between our nodes Bounding[0] and Bounding[1]. I'll show you the rest, just so you get the idea.
//*****************************************************************
TotalTreeID++;
pNode->uiBranches[1] = TotalTreeID;
// Between b[0] and b[1]
BoundingBox[0] = Bounding[0]+((Bounding[1]-Bounding[0])/2);
//Top-Right i.e. b[1]
BoundingBox[1] = Bounding[1];
//middle of node
BoundingBox[2] = Bounding[0]+((Bounding[2]-Bounding[0])/2)+
((Bounding[1]-Bounding[0])/2);
//between b[1] & b[3]
BoundingBox[3] = Bounding[0]+((Bounding[2]-Bounding[0])/2)+
((Bounding[1]-Bounding[0]));
CreateNode(BoundingBox,NodeID,TotalTreeID);
//*****************************************************************
TotalTreeID++;
pNode->uiBranches[2] = TotalTreeID;
//between b[0] and b[2]
BoundingBox[0] = Bounding[0]+((Bounding[2]-Bounding[0])/2);
//middle of node
BoundingBox[1] = Bounding[0]+((Bounding[2]-Bounding[0])/2)+
((Bounding[1]-Bounding[0])/2);
//Bottom-Left i.e. b[2]
BoundingBox[2] = Bounding[2];
//between b[2] and b[3]
BoundingBox[3] = Bounding[2]+((Bounding[3]-Bounding[2])/2);
CreateNode(BoundingBox,NodeID,TotalTreeID);
//*****************************************************************
TotalTreeID++;
pNode->uiBranches[3] = TotalTreeID;
//middle of node
BoundingBox[0] = Bounding[0]+((Bounding[2]-Bounding[0])/2)+
((Bounding[1]-Bounding[0])/2);
//between b[1] and b[3]
BoundingBox[1] = Bounding[0]+((Bounding[2]-Bounding[0])/2) + uiWidth;
//between b[2] and b[3]
BoundingBox[2] = Bounding[2]+((Bounding[3]-Bounding[2])/2);
//Bottom-Right i.e. b[3]
BoundingBox[3] = Bounding[3];
CreateNode(BoundingBox,NodeID,TotalTreeID);
}All we need to do is return nothing and end CreateNode's curly brackets:
return;
}And that's about it. You can download the fully annotated source and executable attached to this article.









Wow amazing article ! I am trying to learn in depth about Quad trees. Can you provide the project file (or a sample project file).
Great work !