so simple euler is
x += v * dt;
v += a * dt;
and all over the web its said that this crops up some errors over time. and NSV is
v += a * dt;
x += v * dt;
and according to this article http://www.brightland.com/physics/ NSV is magnitudes better.....but, why? im writing my dissertation and i feel it would be in my best interest to justify how this is better than euler, besides the fact that its supposedly sympletic, would anyone be willing to give me a more thorough reason? and even why he claims his NSV variant is better which is
v += a * dt * dt;
x += v;
cheers
How is NSV better then euler integration?
NSV has a few nice properties. It exactly conserves momentum, and conserves energy within bounds. In fact, it simulates a slightly different mechanical system (for which it does conserve energy) exactly. It can be derived from a discrete variational principle (are you familiar with Hamilton's Principle?)
A decent place to start is Matt West's Thesis, though more has been done since then.
I also described how to derive NSV from a variational principle in another thread on these forums (EDIT: That's here. EDIT 2: Oh wait, that was your thread too...).... but that said, I think you'll find that in West's thesis too.
A decent place to start is Matt West's Thesis, though more has been done since then.
I also described how to derive NSV from a variational principle in another thread on these forums (EDIT: That's here. EDIT 2: Oh wait, that was your thread too...).... but that said, I think you'll find that in West's thesis too.
well ill have to look up the hamiltonian principle now, but how would you or anyone else describe the vast difference the order of the equation makes? against euler....i'm aware of the results it produces..it's more stable and conserves energy..but why compared to euler since they are nearly identical
cheers
cheers
Quote:Original post by homojedi
well ill have to look up the hamiltonian principle now, but how would you or anyone else describe the vast difference the order of the equation makes? against euler....i'm aware of the results it produces..it's more stable and conserves energy..but why compared to euler since they are nearly identical
Well, one property -- which I've got to admit I don't fully appreciate yet myself -- is that ordering them this way makes the integrator time-reversible (think about it; you can always "backtrack" with NSV but not with explicit Euler). That's the only place where the order of the lines seems to jump out as significant in its own right...
NSV = modified velocity-verlet integrator
It simply makes assumptions about what is being integrated, in this case a constant accelerated body.
While I would not discourage anyone from learning Lagrangian and Hamiltonian mechanics, I think you can get a good bit of understanding by taking a look at the kinematic equation for a body under constant acceleration:
x = x' + v*t + 0.5 * a * t * t
When you combine the NSV integrator you get:
x = x' + v * t + a * t * t
They are the exact same except for a dropped constant.
So the reason NSV is better than Euler because it takes the effect of acceleration over a single time step into account. As for his version of the NSV I don't think it is better.
NSV-His:
x = x' + v + a * t * t
Try testing his with large velocities. I would bet it is far from "better".
It simply makes assumptions about what is being integrated, in this case a constant accelerated body.
While I would not discourage anyone from learning Lagrangian and Hamiltonian mechanics, I think you can get a good bit of understanding by taking a look at the kinematic equation for a body under constant acceleration:
x = x' + v*t + 0.5 * a * t * t
When you combine the NSV integrator you get:
x = x' + v * t + a * t * t
They are the exact same except for a dropped constant.
So the reason NSV is better than Euler because it takes the effect of acceleration over a single time step into account. As for his version of the NSV I don't think it is better.
NSV-His:
x = x' + v + a * t * t
Try testing his with large velocities. I would bet it is far from "better".
Quote:
So the reason NSV is better than Euler because it takes the effect of acceleration over a single time step into account.
okay when i think about it, and look at the euler
x += v * dt;
v += a * dt;
the v that is used is v calculated from the previous timestep and NSV is done in such a way that since x(position) is dependant on velocity ergo acceleration they are calculate before integrating the position, which is more accurate. am i close?
Quote:Original post by homojedi
he claims his NSV variant is better which is
v += a * dt * dt
x += v
So... I just looked at the website you linked to, homojedi, and... the two are the same (up to rounding error).
In the comments, he says "v is prescaled: really a displacement." I.e., really it's not velocity; it's velocity multiplied by dt. So let's stop calling it 'v' and start calling it 'd;' it is related to the actual velocity by
d[k] = v[k]*dt . (1)
Ok? And his integration scheme is,
d[k+1] = d[k] + a[k] dt^2 (2)
x[k+1] = x[k] + d[k+1] . (3)
Well, you can substitute (1) into (2) and (3) to get,
v[k+1] = (1/dt) d[k+1] = (1/dt) d[k] + a[k] dt = v[k] + a[k] dt
x[k+1] = x[k] + v[k+1] dt
which is just the same as the original scheme. He's just rearranged the arithmetic operations a little.
What he's done does have the small advantage of requiring one less multiplication by dt (you just precompute dt^2 once). If his was more accurate in experiments, perhaps that cuts down on rounding error.
yeah i knew it wasent velocity anymore, its displacement 'd' as you said, or if were really pedantic 's'.
but thank you all for your help, although i dont have a full understanding of it i at least have something to talk about
cheers
but thank you all for your help, although i dont have a full understanding of it i at least have something to talk about
cheers
Symplectic integration is important!!
Imagine the state of your system as a point in an abstract "phase space", whose coordinates encode information about both the velocity and position. Then as your particles move around in real space, your system traces out an orbit in the phase space.
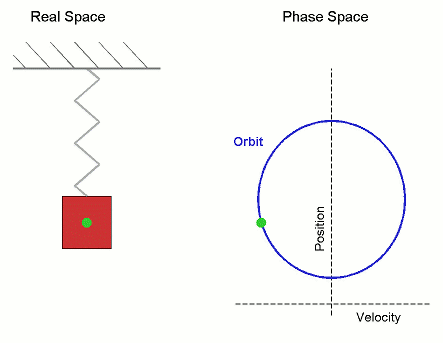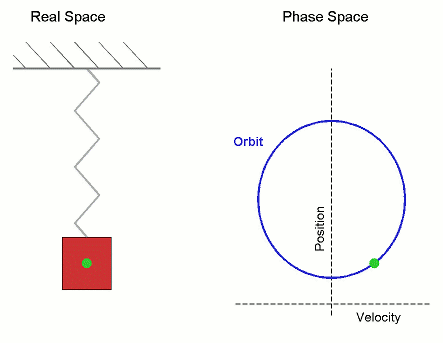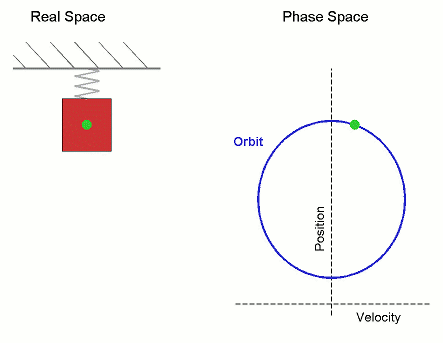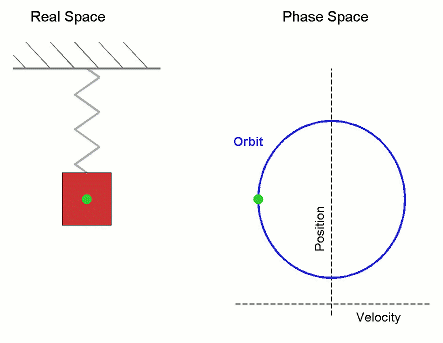
Similarly, every other point in phase space corresponds to another potential "set-up configuration" for your physical system, and the orbits for each possible configuration "foliate" the phase space (like 2D layers cut through and foliate a 3D rock).

For example, the phase-space foliation of the spring system above is a series of concentric circles that cover the plane, with each larger circle corresponding to a spring that was stretched a little bit longer.
Now, for physical systems there are some rules about how the phase space can be foliated. For one, if the system is deterministic then the orbits can't cross each other (to see this, imagine if the system found itself at the point where the orbits cross - which orbit should it follow after that?).
Perhaps less intuitively, one could also imagine tracing out the deformation of an "area" in phase space by tracing the orbit of each point in that area. In other words, we start out with an infinite number of start configurations that are roughly similar, and simultaneously trace out the trajectory of all of them as time progresses. It is an interesting and important fact that, although they may change in shape, these regions in phase space always retain the same area (for classical mechanics). This is what people mean when they say things like "the hamiltonian flow is area-preserving".
Maybe this reminds you of celestial mechanics, where a planet sweeps through the same area every second regardless of what part the elliptical orbit it is in.

However, unlike celestial mechanics, the area we are talking about is in phase space not real space, and the orbit is not the path of a planet in 3D, but rather the path of a system in the higher dimensional phase space. In the spring example, if you started with a blob in phase space, it would stay the same shape but uniformly rotate around the origin.
An integrator also traces out a "path" in phase space, but this path is a series of straight line jumps from one point in phase space to another at each time step. The hope with any numerical integrator is that, as the timesteps get smaller and smaller, the jumpy path better approximates the true orbit in phase space.
If the integrator is to be physically realistic, at the very least it should preserve the topology and of phase space. If the real system foliates the plane into circle-like orbits, then the integrator should as well - turning a circle into a wobbly ellipse is OK, but turning it into a spiral is not.

Similarly, since the true orbits are area-preserving, the simulated ones should be as well (up to machine precision). This is what symplectic integrators do, and why they are important for getting accurate results. (since areas are preserved, you could never, for example have simulated orbits cross; another corollary is better conservation of energy/less dissipation).
Imagine the state of your system as a point in an abstract "phase space", whose coordinates encode information about both the velocity and position. Then as your particles move around in real space, your system traces out an orbit in the phase space.

Similarly, every other point in phase space corresponds to another potential "set-up configuration" for your physical system, and the orbits for each possible configuration "foliate" the phase space (like 2D layers cut through and foliate a 3D rock).

For example, the phase-space foliation of the spring system above is a series of concentric circles that cover the plane, with each larger circle corresponding to a spring that was stretched a little bit longer.
Now, for physical systems there are some rules about how the phase space can be foliated. For one, if the system is deterministic then the orbits can't cross each other (to see this, imagine if the system found itself at the point where the orbits cross - which orbit should it follow after that?).
Perhaps less intuitively, one could also imagine tracing out the deformation of an "area" in phase space by tracing the orbit of each point in that area. In other words, we start out with an infinite number of start configurations that are roughly similar, and simultaneously trace out the trajectory of all of them as time progresses. It is an interesting and important fact that, although they may change in shape, these regions in phase space always retain the same area (for classical mechanics). This is what people mean when they say things like "the hamiltonian flow is area-preserving".
Maybe this reminds you of celestial mechanics, where a planet sweeps through the same area every second regardless of what part the elliptical orbit it is in.

However, unlike celestial mechanics, the area we are talking about is in phase space not real space, and the orbit is not the path of a planet in 3D, but rather the path of a system in the higher dimensional phase space. In the spring example, if you started with a blob in phase space, it would stay the same shape but uniformly rotate around the origin.
An integrator also traces out a "path" in phase space, but this path is a series of straight line jumps from one point in phase space to another at each time step. The hope with any numerical integrator is that, as the timesteps get smaller and smaller, the jumpy path better approximates the true orbit in phase space.
If the integrator is to be physically realistic, at the very least it should preserve the topology and of phase space. If the real system foliates the plane into circle-like orbits, then the integrator should as well - turning a circle into a wobbly ellipse is OK, but turning it into a spiral is not.

Similarly, since the true orbits are area-preserving, the simulated ones should be as well (up to machine precision). This is what symplectic integrators do, and why they are important for getting accurate results. (since areas are preserved, you could never, for example have simulated orbits cross; another corollary is better conservation of energy/less dissipation).
This topic is closed to new replies.
Advertisement
Popular Topics
Advertisement

