Introduction
Many of the beginners on the site are pre-college students. Often beginners will learn by reading tutorials on the Internet, copying code from books, and trying out things that they find interesting. This article is part of a series that focuses on giving pre-college developers the basics they need to understand data structures. The previous article was on Stacks and Queues. This article is about tree data structures.Tree Data Structures
Trees of data are very useful for many things. Since we are a game development site, one of the most common uses of tree data structures is to subdivide space, allowing the developer to quickly find objects that are nearby without having to check every object in the game world. Even though tree data structures are fundamental to computer science, in practice most standard libraries do not directly include tree-based containers. I'll cover the reasons for that in the details.The Basic Tree
A tree is, well, a tree. A real life tree has a root. It has branches. And at the end of the branches it has leaves.
A data structure tree starts at a root node. Each node can branch off into child nodes. If a node has no children, it is called a leaf node. When you have more than one tree, it is called a forest.
Here is an example of a tree. They are generally drawn upside down from real life trees; the root node is usually drawn at the top, and the leaves are usually drawn at the bottom.
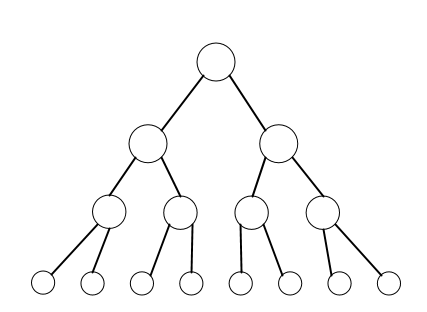
One of the first questions to ask is: How many children should a node have?
Many trees have up to two child nodes. These are called binary trees. The example above is a binary tree. Usually the children are called the left and right child nodes.
Another common type of tree in games has four child nodes. A quadtree, which is a tree that can be used to cover a grid, will usually call the child nodes by the direction they cover: NorthWest or NW, NorthEast or NE, SouthWest or SW, and SouthEast or SE.
Trees are used in many algorithms. You have already heard about binary trees. There are balanced trees and unbalanced trees. There are red-black trees, AVL trees, and many more.
While the theory of a tree is nice, it suffers from some major flaws: Storage space and access speed.
What is the best way to store a tree?
The most basic route, simply building a linked list, is also one of the worst cases you can construct.
Let's assume you want to build a balanced binary tree. You start out with this data structure:
// Tree node
Node* left;
Node* right;
sometype data;
Fair enough.
Now let's assume you want to store 1024 items in it.
So for 1024 nodes you will need to store 2048 pointers. That's fine, pointers are small and you can live with the tiny space.
You may recall that every time you allocate an object it consumes a small amount of additional resources. The exact amount of extra resources depends on the libraries your languge is using. Many popular compilers and tools can use the wide range from just a few bytes to store the data on the small end up to using several kilobytes of padding to help with debugging on the large end. I have worked with systems where even the smallest allocation required 4KB of memory; in this case the 1024 items would require about 4MB of memory.
It usually isn't that bad, but the overhead of lots of tiny objects allocated individually will add up quickly.
Next, the speed issue.
Processors like it when things are right next to each other in memory. Modern processors have a piece of very fast memory --- the cache --- that usually works really well for most data. Whenever a program needs one piece of data the cache will load up that item and also all the items next to it. When something isn't loaded in the very fast memory --- called a cache miss --- it will pause the program until the data is loaded.
The most direct format where every tree item is stored in its own little bucket of memory means that nothing is next to each other. Every time you travel across the tree you end up stalling your program.
So if making a tree directly has these problems, we should consider a data structure that acts like a tree but doesn't have the problems.
Which brings us to...
The Heap
Just to be confusing, there are two kinds of heap. One is the memory heap. It is a huge block of memory where objects live. That is not the kind of heap I am writing about. A heap data structure in concept is the same as a tree. It has a root node, each node has child nodes, and so on. A heap adds constraints that it must always be sorted in a special way. You will need to provide a sorting function --- usually the less than operator. When objects are added or removed from a heap the structure shuffles itself to be a "complete" tree, where every level in the tree is full, except for possibly the last row where everything must be pushed on one side. This makes storage space and searches on a heap very efficient. Heaps can be stored in an array or a dynamic array so there is little space wasted per allocation. C++ provides functions such as push_heap() and pop_heap() to help you implement heaps on your own containers. Java and C# do not provide similar functionality in their standard libraries. 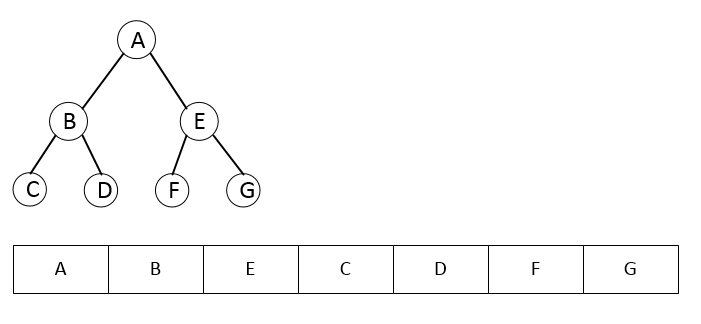Here are a tree and a heap with the same information: