Greetings
Welcome back everyone,
It's time for the second article in the 3D series, in which we cover another basic element of a 3D system... something seen in nearly ever demo for the past few years that involves vectors at all. Rotation. Whether it be that nice texture-mapped stone from Valhalla's "Solstice", or just a flat-shaded cube from a 4k intro, things rotate almost constantly. So it's time to start performing some rotations on our own. :-)
I'm going to keep this article relatively short (along with the subsequent ones)... after all, Snowman has more to put in DemoNews than my constant rambling, and I can't keep sucking up all the space like this. ;) Nonetheless, I hope you find this article useful, as we continue our drive toward learning 3D graphics.
Ready? Well like it or not, here we go!
Section One - 2D Rotation
Before we can get more sophisticated 3D rotations going, we need to try it in two dimensions first... because 3D rotations are just based on three 2D rotations, but combined.
So how do we rotate something in 2D? How do we take any 2D point, give it an angle to rotate by about the origin, and get it correctly to its new position? Well this is where that Trig knowledge from the first article comes into play.
Everything about rotation involves Trig. Sine and Cosine are very much your friends here. And it's not that complicated, really... you can rotate in one plane with only 4 multiplies (other optimizations come later as well).
So how do we go about this? Well, let's take it piece by piece. First, I'll assume the XY plane (the real one, where Y goes up) for this, as we try to take a point and rotate it.
A lot of docs, when trying to explain rotation, will give you the simple equations for it but give you no clue as to how those equations came about. Several people have asked me, "Hey, if and when you ever do a 3D tutorial, tell me how the heck you get those rotation equations, cuz I have no idea where those came from and why they work."
Well, I can't quite tell you where they came from at first (like who thought of them), but I can replicate the ideas here and show you what makes sense to me. If it makes sense to you to, then I guess it worked. :-)
Here's the idea...
Get out a piece of paper. No, don't worry, this isn't a quiz. ;)
On the paper, draw a pair of conventional XY coordinate axes, and then lightly sketch a large circle on it. Make sure the circle is light; you don't really need it for much except placing a couple points.
After you draw the circle, put a point at about, say, 30 degrees (assuming 0 degrees is to the right and the angles go counterclockwise). Then put another point at about 70 degrees, in the same fashion. We're going to pretend that the first point is our original point, and that we're trying to rotate it to the second point, our destination... a rotation of 40 degrees about the origin. The actual accuracy of the points doesn't matter; if you're a bit off, it's fine.
Now with each point, draw a triangle for that point. Each triangle's three sides are the X axis, the the line from the origin to the point, and the line from the point straight down to the X axis. What you should have now are two right triangles in the upper right quadrant of your XY plane, one being pretty upright (the destination point's), and the other a bit more wide than tall.
Time for some labels... okay, for each triangle, label the line going from the origin to the point as "R" (for radius). Since it's the same length for both triangles, we use the same label. Now, on the first triangle (the short, wide one), label the side along the X axis "X", for that length. Likewise, label the line from the X axis up to the point as "Y" for that height.
For the second triangle (the tall one, for the 70 degree point), label the X length and Y height as "U" and "V", respectively, in a similar fashion.
Finally, we need two angles. In the angle between the X axis and the first, lower R side (30 degrees), label it f (called Phi). Then label the angle between the lower R and the higher R (the one at 70 degrees) as q (called Theta).
There we go... we've got our drawing. :-) If my little walkthrough in drawing this has confused you to no end, either try it again from the beginning, or look at the PCX in this supplement, with an image of the same diagram I'm describing.
Okay, so we have this drawing. Basically, what we know in the beginning is that we have this initial point at an unknown angle (we know it's 30 degrees in this example, but normally, you won't know that for arbitrary points), yet we know it has Cartesian coordinates (X,Y). What we want to do is pump X and Y through an equation or two, along with the angle we want to rotate by (which we labeled as Theta, and in this example is 40 degrees), and find out its new coordinates, called (U,V). So what equations do we use? Let's find out...
There are several convenient identities in Trigonometry that you can find in pretty much every math textbook with Trig in it.... one of those identities is called the "Law of Sines", which goes like this...
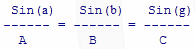
Where A, B, and C are the lengths of the sides of a triangle, and a, b, and g are the angles directly opposite those sides...

It doesn't have to be a right triangle; it works for every triangle there is. Granted, for our purposes, we will be using our right triangles, and this will help us out.
Now if we use our first right triangle, the short one, and pretend that R is our "C" of the triangle, by the fact that this is a right triangle, we know that g is 90 degrees. And the Sine of 90 is 1, which gives us one very nice piece of math meat.
We only need to use one other side of our Law of Sines formula in this example, in this case, the A-a side. In our case, "A" is the same as Y, and a is the same as f. So we have a little mini-formula,
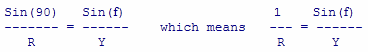
Then, if you multiply each side by Y, it moves the Y to the left side, so
Y
--- = Sin(f)
RThis should all make sense so far, I hope. If you're looking at the diagram as you read this, it should clear things up a bit.
Okay, so we can see the relation between the angle f, and the sides Y and R. Well since f is across from Y, shouldn't we be able to have the same kind of relation for the other triangle, with V and R? The angle across from V is just f and q added together, so shouldn't that work?
Sure does. :-)
V
--- = Sin(f+q)
ROkay, time for another nifty Trig identity (BTW, if you don't have a math book with all these identities in it, let me know... if enough people ask for a listing, I'll type up a quick reference list with identity equations that you can use. Just email to the address at the end, if you think you'd like that
Anyway, another nice identity is that for any two angles a and b,
Sin(a+b) = Sin(a)*Cos(b) + Cos(a)*Sin(b)So we sub that into our previous thing, and we have
V
--- = Sin(f)*Cos(q) + Cos(f)*Sin(q)
RMultiply by R now, to get V (the destination point's X value that we've been trying to find), and it's
V = R*Sin(f)*Cos(q) + R*Cos(f)*Sin(q)Welp, last identity.... this one, taken from Polar coordinates. If you've had algebra, you've used Polar coordinates before. Well if you remember the way to convert a polar point to Cartesian (I doubt you do, so I'll remind you... it's gonna take a while before you end up memorizing all these darn formulas, trust me those conversions are
X = R*Cos(Theta) *** Don't confuse these with our R, X, or Y!
Y = R*Sin(Theta) They're just conversion equations ***Well look at our V equation above... notice anything? We know Phi is an angle in the triangle that deals only with X and Y, which we know (since they're just your first point and all). So can we drop those R*Sin(f) and R*Cos(f) parts and just sub in X and Y like you would do with Polar? You betcha...
V = Y*Cos(q) + X*Sin(q) *** FINAL V EQUATION!!! ***That's all we need! Hooray!
We know X and Y, since we started with those. And we know q, since it's the number of degrees we want to rotate by (in our example, 40 degrees). So if we use this equation, we get the V value, which is the Y coordinate of the FINAL point.
Now we still need to get U (the final point's X coordinate). Luckily, the series of equations is the same almost, except one identity is different. I won't work out the whole thing again, you can do that if you want. But here are the differences that you'll see. One, since we're doing the horizontal element instead of vertical,
U
--- = Cos(f+q)
RNow Cosine's Sum of Angles formula is a little bit different than Sine's,
Cos(a+b) = Cos(a)*Cos(b) - Sin(a)*Sin(b)which will end up giving us that subtraction instead of addition in the end. If you keep working the equations the same as we did before, but with this new identity, you get the U equation too!
U = X*Cos(q) - Y*Sin(q) *** FINAL U EQUATION!!! ***Summing up those equations into nice, happy, 2D rotation form.....
NewX = (OldX*Cos(Theta)) - (OldY*Sin(Theta))
NewY = (OldY*Cos(Theta)) + (OldX*Sin(Theta))And there we have it! Note that I made it very clear as to the difference between the "Old" and "New" values. It's important that you do this, too. You don't want to just use a value "X", for example.... because if you calculate the "new" X and end up using that instead of the "old" X in the second equation (for NewY), you don't get the right rotation.
IN ROTATION, USE ONLY THE OLD VALUES UNTIL ALL THE NEW ONES ARE FOUND!
Once you have the final new X and Y values, THEN replace the old pair with the new pair, and go on your way. Make sure to keep the values separate until that time.
BTW... As you look back at how I derived these rotation formulas, don't feel bad if you feel like you couldn't have derived them yourself... especially if you're just beginning. I know I ran on these formulas blindly for over a year before I ended up losing them and was forced to recreate them again in this fashion. I couldn't have done it earlier. It takes time, so if you feel like you're still in the dark... don't. Eventually you'll get the hang of it all. :-)
Any more to 2D rotation? Nope, that's the whole of it. Before you try out 3D rotation (explained in the next section), test out the above principles in some of your own code, by plotting a few pixels here and there and then rotating them about the origin. It's not hard at all to turn the above formulas (formulae?) into code. Also, if you need some help or are just plain curious, I've got some example source (in both Pascal and C, just like last time) in this supplement, demonstrating this stuff. Feel free to check it out.
Okay, well, enough of this planar stuff.... on to 3D rotations! (And relax, there's not much more; you've done the bulk of the work already...)
Section Two - 3D Rotation
So what do we need to turn our rotations into 3D rotations? Not much, actually. There are many ways to do rotations in 3D, some simpler than others. The simplest (and most common from what I've seen) way is to do it by using three 2D rotations, one for each axis.
The 2D rotations we did in the last section are on the XY plane. But as you think about the XY plane in terms of 3D, the rotation takes on another meaning... it was also a rotation ABOUT the Z axis. Meaning that we have the Z axis, and whatever Z values the points may have, they stay the same, as we are rotating around that axis itself. The only values that change in a rotation about any axis are the values of the two OTHER coordinates.
So a rotation about Z will affect X and Y, a rotation about X will affect Y and Z, and a rotation about Y will affect Z and X. It's just one big cycle...
So if we want to do a full all-axis 3D rotation, we just arrange three back-to-back 2D rotations, one for each axis, like this...
NewY = (OldY*Cos(ThetaX)) - (OldZ*Sin(ThetaX)) ** X axis rotation **
NewZ = (OldZ*Cos(ThetaX)) + (OldY*Sin(ThetaX))
(Copy NewY and NewZ into OldY and OldZ)
NewZ = (OldZ*Cos(ThetaY)) - (OldX*Sin(ThetaY)) ** Y axis rotation **
NewX = (OldX*Cos(ThetaY)) + (OldZ*Sin(ThetaY))
(Copy NewZ and NewX into OldZ and OldX)
NewX = (OldX*Cos(ThetaZ)) - (OldY*Sin(ThetaZ)) ** Z axis rotation **
NewY = (OldY*Cos(ThetaZ)) + (OldX*Sin(ThetaZ))
(No copies needed, since we're done)The reasons for mid-copies are like I said; for each axis rotation you need to keep using the old values until both the new ones are done. But each axis's rotation is independent of the other two... so after each pair, you need to update all the values before going on to the next axis. You don't want to use one axis's old values when going into rotating about another axis; that would be bad.
Once you've done all three axes, you should have your new point, completely rotated about each angle as you wish (ThetaX, ThetaY, and ThetaZ).
One important point... the order in which you do these axes DOES make a difference. Rotating in an X-Y-Z sequence will not give you the same results as rotating in a Z-X-Y sequence, etc. Now, for your engine at this point, all you're probably concerned about is looks, i.e. that your object is rotating and you can see it rotating. Since that's the case, it really doesn't matter for the moment which order you do things in. It's the appearance that counts. But later on, when you get into more complex issues that involve more things than just a set of points, you'll want to keep your rotation order consistent. I just use X-Y-Z because it's pretty natural. :-)
I'm not going to get into optimizations of this rotation material until another time, but I can give you a hint or two now... first, you'll notice that right now it's at 12 multiplies for a full rotation (4 for each axis). But it turns out you can reduce it to at least 9 multiplies, by precalculating a few values at the beginning of each frame and getting a final 3x3 matrix for the actual point rotations themselves (if you don't know what I mean by matrix, don't worry about it at the moment; we'll get into matrices later on). It's something to look into, if you're curious and feel like tinkering with the math a bit.
Also, once again, this method of rotation is only one way to rotate. There are other ways, sometimes involving other coordinate systems, that can be more efficient on occasion as well. You'll discover those in time (and probably in some of the later articles).
But for now, this I think is the simplest way to begin... get these concepts down first, and drill them into your brain. You'll know when to switch gears when the time comes.
Well, looks like the end of another article! I've got some sample source in this supplement, as well as a PCX of that 2D rotation diagram, if you got lost in all of this mess. :-) Take the time to look at the code, see how it relates to the math used in here, and most importantly, DO SOME EXPERIMENTATION ON YOUR OWN. This kinda stuff isn't learned by reading, it's learned by doing.
Now go forth, plot some dots, get them spinning, and have fun! Keep watching, though... 'cause it's only gonna get better. :-)
See you next time...
Chris Hargrove
a.k.a. Kiwidog, of Terraformer & Hornet
Coding & Organization


"Okay, so we can see the relation between the angle f, and the sides Y and R. Well since f is across from Y, shouldn't we be able to have the same kind of relation for the other triangle, with V and R? The angle across from V is just f and q added together, so shouldn't that work?
This is so confusing I don't see how the angle across from V is IS q, and besides that, f + q is 110 degrees? Could you please put a bit more detail in to that part. It would be great :)