Triangle Plasma
(reposted from here)A couple of months ago, out of boredom, I implemented the old plasma fractals algorithm that is emblematic of the late...
·
2.5k
·
1
The Curiously Recurring Gimlet Pattern
Member since Nov 2009
All Posts
Is there a hexagonal analog of Conway's Game of Life?
The short answer is that in the hexagonal case the best analog of Conway's Game of Life -- in my opinion as someone who has been a CA hobbyist for 30...
·
6.5k
·
1
Triangular Life
Recently I looked through a bunch of triangular cellular automata in which each (1) uses two states, (2) uses the simple alive cell count type of...
·
3.1k
Lifelike, or the Joy of Killing Time via Breeding Little Squiggles
[color=rgb(40,40,40)][font='Times New Roman']A couple of weeks ago I got interested in this project but wanted full control of the code, wanted to...
·
4.2k
draak update
[color=#282828][font='Times New Roman']Below is gameplay video of a prototype of the puzzle game "Draak" that I am working on. Draak will be an...
·
3.6k
My Code for Doing Two Things That Sooner or Later You Will Want to do with Bezier Curves
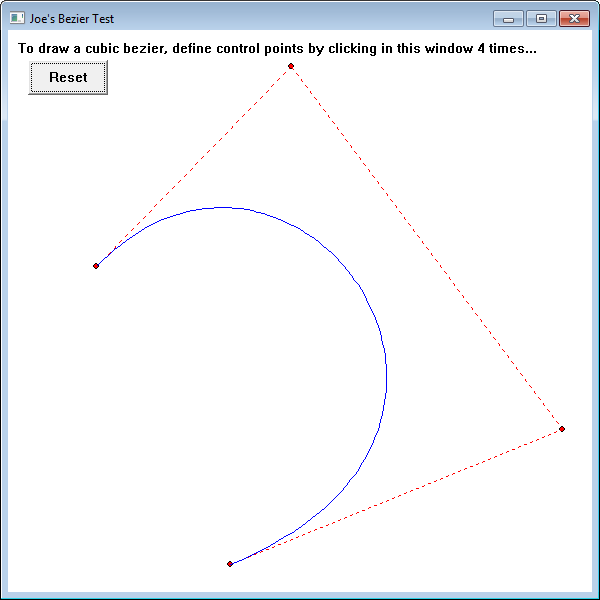
I just added full cubic bezier curve support to the vector tessellation creation tool I am developing (see here). I'll include some video at a later...
·
5.3k
Untitled Escher Game Update
[font='Times New Roman']I've decided my "[/font]untitled Escher game[font='Times New Roman']", i.e.[/font] Zoop[font='Times New Roman'] on a double...
·
3.5k
·
1
An Application for Creating Novel Escher-like Tessellations of the Plane
Over the past several weeks I have been investigating desktop applications for creating novel Escher-like tilings of the plane. Basically I've...
·
4.7k
·
2
What I am working on
[color=rgb(51,51,51)][font=Georgia]I'm working on a puzzle game for iPads that takes the mechanics of a somewhat obscure game from the 1990s(*) and...
·
3.4k
·
2
Discretely Distributed Random Numbers in C#
Random numbers generated from a discrete distribution are commonly needed in game development.By "discrete distibution" we just mean the roll you get...
·
6.9k
·
2
Cocos2d-x + Box2d Breakout Updated
Cocos2d-x releases since version 3 have broken compatibility with old tutorials. This can especially be a problem when you want to do something...
·
3.1k
·
3
Zzazzy 1.0.0
My iPad game Zzazzy has made it through the review process and is now on the App Store: see here.I will be updating the page I have for it here this...
·
3.2k
·
4
Snurtle and My Greatest Contribution to Mathematics, Such That It Was
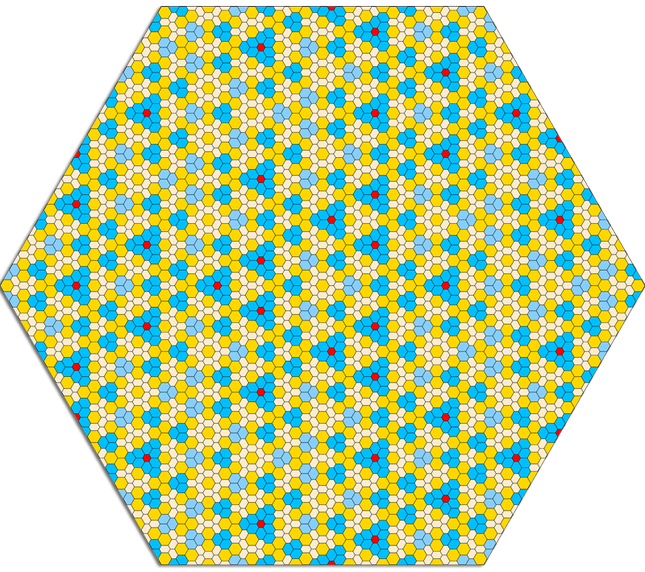
This summer coming up will be 20 years since the summer after I graduated from college. I'm currently in that golden period in between software jobs...
·
3.5k
·
2
New Zzazzy screenshot
Here is what the game is looking like currently (click for full size):Source
·
2.1k
·
2
The World
For the game I'm working on I need to have sprites that travel along curving paths.I'm talking about the sprites traveling along somewhat arbitrary...
·
3k
·
2
Syzygy Update
So, looking at the early entries of this blog, I must have started working on Syzygy around the beginning of the year 2012 because by March 2012 I...
·
2.8k
·
4
Marble Madness Madness
gamedev.net recently linked to this video about the making of Marble Madness, which got me thinking about the raster-to-vector via contour extraction...
·
4.9k
·
2
Sprite Packing in Python
I've been working on my puzzle game Syzygy again, after a long hiatus, and am now writing to iOS/cocos2d-x rather than just working on the prototype...
·
5.1k
The Cocos2d-x Device Orientation Bug
This took me all morning to figure out. I'm posting here so there is clear information on this subject in at least one place on the internet. The...
·
2.8k
Thoughts on porting Syzygy to iOS
I've started trying to figure out the way in which I'm going to port Syzygy to iOS. I don't actually own a Mac -- though I may get one this weekend...
·
3k
Advertisement