I recently started reading the book Artificial Intelligence for Humans, Volume 1: Fundamental Algorithms by Jeff Heaton. Upon finishing reading the chapter Normalizing Data, I decided to practice what I had just learnt to hopefully finally understand 100 % of a special algorithm : …

Subscribe to our subreddit to get all the updates from the team!

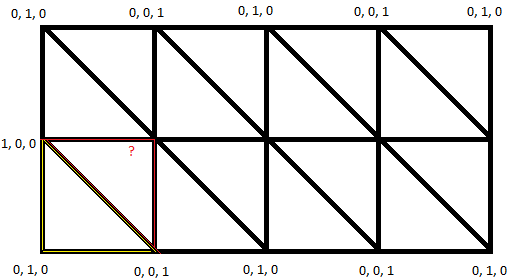
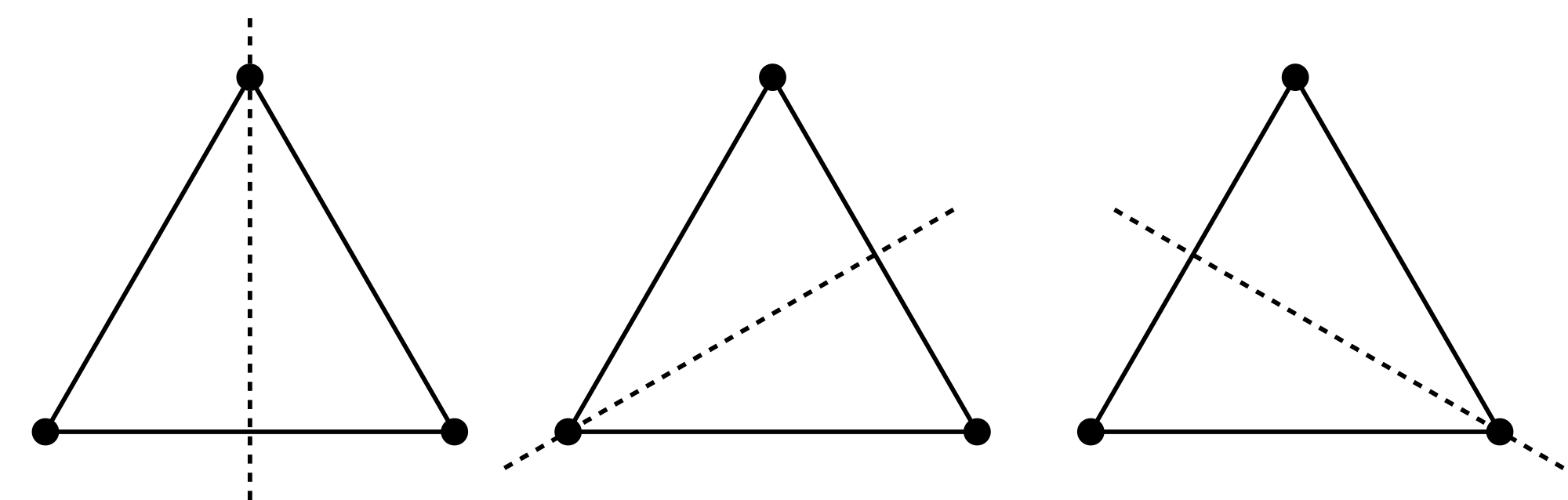
In our 3D game (miimii1205), we use a dynamically created navigation mesh to navigate onto a procedurally generated terrain. To do so, only the A* and string pulling algorithms were…

Subscribe to our subreddit to get all the updates from the team!

Last month, I made a pretty simple dungeon generator algorithm. It's an organic brute force algorithm, in the sense that the rooms and corridors aren't carved into a grid and that it stops when an area doesn't fit in the graph.…

Subscribe to our subreddit to get all the updates from the team!

First off, here's a video that shows the unit vision in action : 

So, what is the unit vision? It's a simple mechanism that notifies a unit when another unit enters its vision field. It also takes into accou…

Subscribe to our subreddit to get all the updates from the team!

I have integrated the zone separation with my implementation of the Marching Cubes algorithm. Now I have been working on zone generation.

A level is separated in the following way :

Subscribe to our subreddit to get all the updates from the team!

Recently I've been tackling with more organic low poly terrains. The default way of creating indices for a 3D geometry is the following (credits) :

A way to create simple differences that makes the geometry slight…

Subscribe to our subreddit to get all the updates from the team!

A friend and I are making a rogue-lite retro procedural game. As in many procedural rogue-lite games, it will have rooms to complete but also the notion of zones. The difference between a zone and a room is that a zone is open air whil…

I integrated LibGDX's Behavior Tree AI module into our roguelite, vaporwave and procedural game, which is made use the jMonkey Engine 3.1.

I then created the following behavior :

- Follow enemy

- Search the enemy's last recorded position

- Return back to initial chase position

- Stop the chase after a c…

Today, I finally finished the following features :

Here is a video demonstrating those features :

For more information and updates about the game, which is a voxel colony simulation / survival, please subscribe to r/CheesyGames.

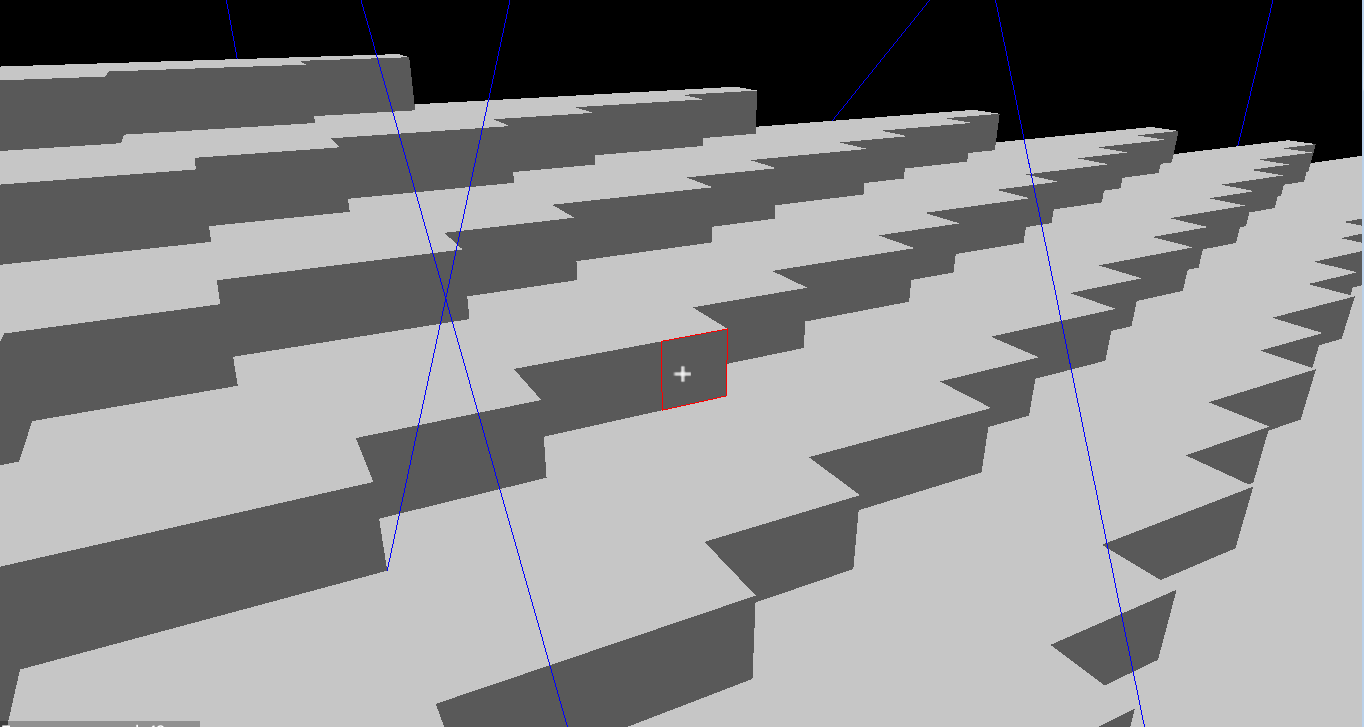
This is a simple world made of chunks of 32³ voxels. The world itself is not static : as you can see on the top of the image, chunks only exist if there …

Subscribe to our subreddit to get all the updates from the team!

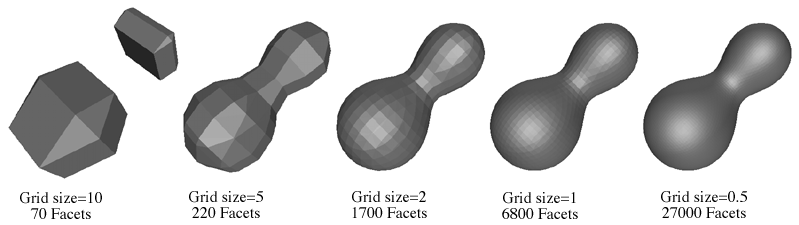
I have had difficulties recently with the Marching Cubes algorithm, mainly because the principal source of information on the subject was kinda vague and incomplete to me. I need a lot of precision to understand something complicated :…

So we had our first hater... but first please listen to one of our music we think we was bashing against. After that, let's hear the context.

Our development blogs on gamedev mainly focus on the actual development of our game(s) and any related research that we've done. So, our t…

Subscribe to our subreddit to get all the updates from the team!

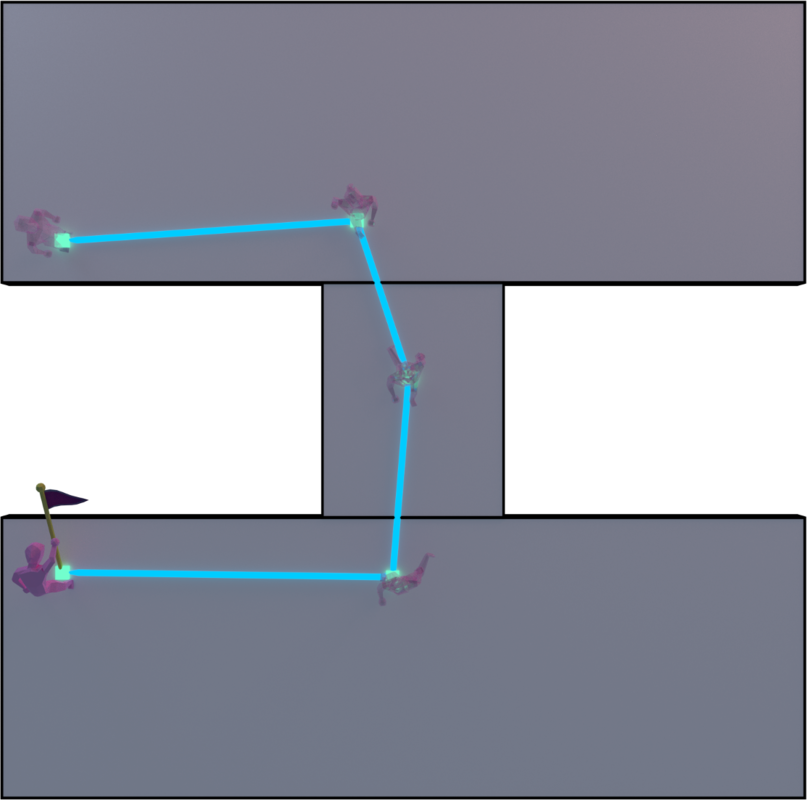
We wanted units in our game to be able to pick up items, including the player. But how can the player know which item will be picked up when he executes that action? Traditionally, video game developers and designers do this by usi…

Voxels! Unlike my old XNA application, this one's code is way more beautiful to the eye. Zero switch or if and else for cube faces, as I did with my cubic planet faces.

My only problem with voxels is that it's a 3D grid. A 3D grid take a lot longer to compute than six 2D grids.
250 * 6 = 1500 quads t…

I'm an amateur and hobbyist video game developer. I've been programming for 9 years now even though I'm almost 21. When I started, it was rough being extremely bad with the English language and a noob programmer. Instead of helping me, people over multiple forums were only degrading my lack of skil…