Skip to main content
GameDev.net gamedev.net
🔒 Locked

Find Collision response of two objects

Started by knonk Apr 13, 2009 at 4:12 AM 21 replies 14.3k views
Original Post
knonk
knonk
Hi, how can i find collision response between rectangle and circle like in this picture : i want to identify the direction and magnitude of V1 vector and the V2 vector after they collided , With : + V1 : initial veloc vector of Circle + M1 : mass of Circle + V2 : initial veloc vector of Rectangle + M2 : mass of Rectangle does anyone have some idea about this ? [Edited by - knonk on April 15, 2009 2:26:36 AM]
oliii
oliii
picture not working.
Everything is better with Metal.
Winegums
Winegums
You mgiht need to be logged into physicsforums.com to view the picture...that or they just flat out block hotlinking (it's still called that isn't it?).
oliii
oliii
well, no pics, so I'll stab in the dark.

to find the intersection of a sphere and triangle, you need to find the point on the triangle periphery the closest to the sphere centre.

Once you have that point, it is straight forward to find the two contact points.

as for the response, given mass and velocity of the two objects, there's been many discussions about that, some from last week.

example :

bool applyReponse(RigidBody& a, RigidBody& b, const Vector& mtd){    // inverse masses (for static objects, inversemass = 0).    float ima = a.m_inverseMass;    float imb = b.m_inverseMass;    float im  = ima + imb;    if(im < 0.000001f) im = 1.0f;    // separate the objects so they just touch each other    const float relaxation = 0.8f; // relaxation coefficient, arbitrary value in range [0, 1].    a.m_position += mtd * (ima / im) * relaxation;    b.m_position -= mtd * (imb / im) * relaxation;    // collision plane normal. It's the mtd vector, but normalised.    Vector n = mtd;     n.normalise();    // impact velocity along normal of collision 'n'    Vector v = (a.m_velocity - b.m_velocity);    float vn = v.dotProduct(n);    // objects already separating, no reflection    if (vn > 0.0f) return true;    const float cor = 0.7f; // coefficient of restitution. Arbitrary value, in range [0, 1].      // relative collision impulse    float j = -(1.0f + cor) * vn / (im);      // apply collision impulse to the two objects    a.m_velocity += n * (j * ima);    b.m_velocity -= n * (j * imb);    return true;}
Everything is better with Metal.
knonk
knonk
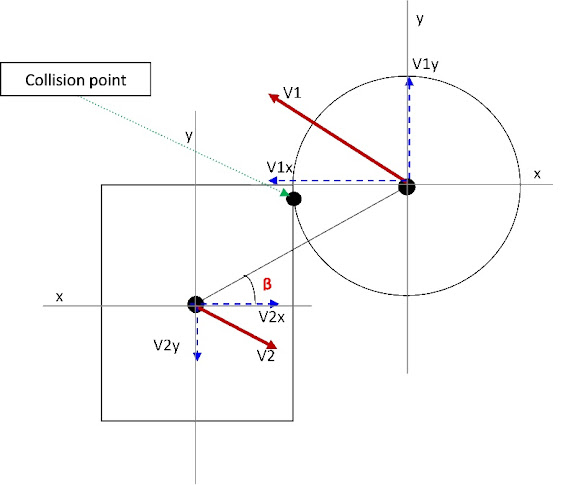
Oh, Thank's for your explaination so much, Oliii. I will show the picture more clearly :
Please look at this picture :



We consider that :
V1 : veloc vector of circle BEFORE they collide
V2 : veloc vector of rectangle BEFORE they collide
and I have to find v1f,v2f with :
v1f : veloc vector of Circle AFTER they collide
v2f : veloc vector of Rectangle AFTER they collide

This is the oblique collision and the contact point(the collision point) of two object doesn't lie on line of action(the line from center of circle to center of rectangle), I did try some way, but it didn't response as real as i want,Could you explain more clear about this for me please !

[Edited by - knonk on April 15, 2009 2:47:05 AM]
Codeka
Codeka
The picture doesn't display if you're not logged into the physicsforums.com website. I don't have an account there, so I can't see the picture at all. I would suggest you upload the picture to flickr or photobucket or some other site where we can see it without having to sign up...
knonk
knonk
Oh,Im sorry, I did post to google, so hope u can see it :
Please look at this picture :


We consider that :
V1 : veloc vector of circle BEFORE they collide
V2 : veloc vector of rectangle BEFORE they collide

and I have to find v1f,v2f with :
v1f : veloc vector of Circle AFTER they collide
v2f : veloc vector of Rectangle AFTER they collide

This is the oblique collision and the contact point(the collision point) of two object doesn't lie on line of action(the line from center of circle to center of rectangle), I did try some way, but it didn't response as real as i want,Could you explain more clear about this for me please !
oliii
oliii
I thought that function closestPointToRectangle () was relatively clear.

basically, you find the point on the rectangle contour the closest to the sphere centre, which is what the code does above, and that gives you the collision point.

once you have that point, then you can apply the collision response above, which is based on the conservation of momentum.

the MTD is bascially the vector separation between the two points of contact on the objects. Since your objects are not intersecting, the MTD will be zero, so you'll need another way to find the collision normal. In case of a sphere, it's quite simple, it's just the vector (V1 - sphere.centre), normalised.

then the complete response code would be :

Vector closestPoint(const Vector& p, const Rectangle& r){    // relative position of sphere centre from the rectangle centre    Vector d = (p - r.m_centre);    // rectangle half-size    Vector h = r.m_halfSize;    // special case when the sphere centre is inside the rectangle    if(fabs(d.x) < h.x && fabs(d.y) < h.y)     {        // use left or right side of the rectangle boundary        // as it is the closest        if((h.x - fabs(d.x)) < (h.y - fabs(d.y)))        {             d.y = 0.0f;             d.x = h.x * sign(d.x);        }        // use top or bottom side of the rectangle boundary        // as it is the closest        else        {             d.x = 0.0f;             d.y = h.y * sign(d.y);        }    }    else    {        // clamp to rectangle boundary        if(fabs(d.x) > h.x) d.x = h.x * sign(d.x);        if(fabs(d.y) > h.y) d.y = h.y * sign(d.y);    }    // the closest point on rectangle from p    Vector c = r.m_centre + d;    return c;}bool applyReponse(sphere& a, rectangle& b, const Vector& normal){    // inverse masses (for static objects, inversemass = 0).    float ima = a.m_inverseMass;    float imb = b.m_inverseMass;    float im  = ima + imb;    if(im < 0.000001f) im = 1.0f;    // impact velocity along normal of collision 'n'    Vector v = (a.m_velocity - b.m_velocity);    float vn = v.dotProduct(normal);    // objects already separating, no reflection    if (vn > 0.0f) return true;    const float cor = 0.7f; // coefficient of restitution. Arbitrary value, in range [0, 1].      // relative collision impulse    float j = -(1.0f + cor) * vn / (im);      // apply collision impulse to the two objects    a.m_velocity += normal * (j * ima);    b.m_velocity -= normal * (j * imb);    return true;}void collisionResponse(sphere& s, rectangle& r){    Vector closest = closestPoint(s.m_centre, r);    Vector normal = (s.m_centre - closest);    normal.normalise();    applyReponse(s, r, normal);}


Everything is better with Metal.
knonk
knonk
Hi Oliii,
I did try to read your explain but still don't get it clearly,
Let me say again your method :

1) Finding the closest point between rectangle and sphere, also is collision point

2) Apply the collision response from collision point

Is it right?, I don't understand from second step in your explain(It's easier to understand if u could explain more clearly here) ,Could you tell me more clearly and basically your method,please !
oliii
oliii
Quote:
Original post by knonk
Hi Oliii,
I did try to read your explain but still don't get it clearly,
Let me say again your method :

1) Finding the closest point between rectangle and sphere, also is collision point

2) Apply the collision response from collision point

Is it right?


Yup. That's the standard collision detection and response process. What you also need is the collision normal, so you can apply a collision impulse.

Quote:
I don't understand from second step in your explain(It's easier to understand if u could explain more clearly here) ,Could you tell me more clearly and basically your method,please !


Well, I'll give it a shot.

taking my cues from

http://chrishecker.com/images/e/e7/Gdmphys3.pdf

Friction aside, when objects collide, their linear momentum (in short, velocities) will change along the normal of collision. The amount of change to apply to the two objects depends on a few parameters, such as the direction of the collision (defined by the collision normal vector), the object's respective mass (when colliding heavy objects against light objects, the light objects will be the most influenced by the collision), and the objects' respective velocities.

a collision impulse is like an instantaneous force. It affects the momentum (velocities) of objects directly.

v' : new velocity after impulse
v : velocity before impulse
i : impulse vector
m : object mass

v' = v + i / m

when two bodies collide, the impulse applied on object a will be transfered to the object b, but opposite (Newton 3rd law). The impulse vector i will be an impulse amount along the normal of collision n, so you get.

(eq1) va' = va + (j * n) / ma
(eq2) vb' = vb - (j * n) / mb

for the final equation, the effect of a elastic collision on two objects velocity will be such as :

(eq3) (va' - vb') . n = -(va - vb) . n

the relative velocity is basically reflected (imagine a particle hitting a static object, the particle velocity will be flipped along the normal of collision, hence reflected).



if you want some energy loss, and a more realistic effect after collision (there will always be some energy lost after a collision, in the form of heat, sound, and magical dust).

(eq4) (va' - vb') . n = -cor * ((va - vb) . n)

cor is the coefficient of restitution, in the range [0, 1].

so, you have three unknowns (va', vb', j) and three equations (eq1, eq2, and eq4).

substitute va' and vb' from eq1 and eq2 into eq4, and you'll get

[va + (j * n) / ma - vb + (j * n) / mb] . n = -cor * [(va - vb) . n]

so now, you can solve that equation, and get a value for j.

j = - (1 + cor) * [(va - vb) . n] / [(n.n) * (1/ma + 1/mb)]

apply j in (eq1) and (eq2), and you get the new velocities for both objects.

In your example, the collision point is used to work out the normal of collision, which will be the vector passing through the collision point, and the sphere centre.

n = (ball.centre - collision_point);

preferably normalised.
Everything is better with Metal.
knonk
knonk
Oh,yeah. I got it Oliii, I did try to make an example, everything seem is working well but still have a problem that i really can't understand.
I made a Sphere and Rectangle and let them move freely and touch to each other sometime. At the beginning, everything is seem working very well, but sometime, Sphere moved to overlap to Rectangle but I'm sure that my detect collision function worked very well and called collision responding function exactly time when the collision between them happened. But i don't know how can them moved to overlap each other, I'm afraid of the collision responding did something wrong and i did check it again and i got this result :
/* Debugger message */
+ Current Position Rectangle :(x=70.62275585330714, y=71.90892992031561)
+ Current Position Ball :(x=172.3128183554728, y=86.11117117350611)
+ Ball init veloc = (0.22854066073324542;-0.1321411902983307)
+ Rectangle init veloc = (0.0001805809570312178;1.8682677768469214)
+ Collision point = (x=136, y=86.11117117350611)
+ Collision normal = (36.312818355472814;0)
+ Collision normalize = (1;0)
+ v = (0.2283600797762142;-2.000408967145252)
+ vn = 0.2283600797762142
/* End message */
At the time 2 objects collided,they were overlap a little already and the collision response function have to process to separate them far away, but it can't because of this code :>> if (vn > 0.0f) return true;
the value of 'vn' variable in my debug message > 0 thus function was broke and return, and it made 2 objects continuously overlap to each other, I thought.
Did i do something wrong ? please give an advisement !
oliii
oliii
It's possible I got the sign of the normal wrong. Your normal should point roughly, from object B centre towards object A centre. It depends if object A is the rectangle, or the sphere. try flip the normal around (Collision normal = (-36.312818355472814;0)).

the (vn > 0) check is to ensure that the response is not applied when objects separate (their velocity may be opposite, but they are still overlapping). If that is not checked, the objects will get 'sticky'.

Note that you will also ideally want to stop the objects from intersecting at the moment of collision. for that, you need to work out the two contact points on the two objects. You already have the contact point on the triangle, the contact point on the sphere should be dead simple.

that's what this code does

  // separate the objects so they just touch each other    const float relaxation = 0.8f; // relaxation coefficient, arbitrary value in range [0, 1].    a.m_position += mtd * (ima / im) * relaxation;    b.m_position -= mtd * (imb / im) * relaxation;


the MTD is the minimum translation distance, and it's basically, the vector with minimum length you need to apply to have the objects just touching each over and not overlapping. You can work it out by using the contact points (mtd = (contact_on_b - contact_on_a).

but usually, it's done the other way round. You have the mtd computed in the collision detection, then you find the contact points from it.

Also, you can use the mtd as your collision normal, which is what I do initially.

http://www.metanetsoftware.com/technique/tutorialA.html
Everything is better with Metal.
knonk
knonk
Well, I tried to debug many times and I found two problems :

First, that's what I just told you before, there are some positions and sometimes,2 objects actually collided but "Vn" value still > 0, this made them overlap to each other without collision responding, but just sometimes and some positions, this made me so headache.Furthermore,In collision of 2 Rectangles,I think that, the collision normal vector should square to Collision Edge of each Rectangle, Right? It's should look like in this picture :



But this is what im doing :



and you know,even they were not square because in picture, i do :
collision normal vector = Recangle2.CenterPoint - CollisionPoint
So in case of 2 rectangles don't touch each other directly and opposite, the collision normal vector never square to Collision Edge on rectangle,
but in many situations,the collision responding is also right and no overlap happens ! really don't know why.

Second,I let rectangle move to collide circle with velocity of rectangle is greater than velocity of circle 5 times. After collision, the velocity of circle should be increased very a lot, but Actually, it just increased very a little, thus circle seem still move with the same velocity before,still move slowly, and Rectangle have to overlap to circle on the way its moving after colliding.

[Edited by - knonk on April 17, 2009 6:32:19 AM]
oliii
oliii
best I can do is provide you with some code. There could be a sign problem, or a bug... This is more like pseudo code than anything else.

Gimme a minute...
Everything is better with Metal.
oliii
oliii

there you go...

OpenGL / glut, tested with visual studio 8.

#include <windows.h>#include <gl\glut.h>#include <math.h>#include <stdio.h>#include <stdlib.h>#pragma comment (lib, "opengl32.lib")#pragma comment (lib, "glu32.lib")#pragma comment (lib, "glut32.lib")float sign(float a)								{ return (a>0)? 1.0f : -1.0f; }float clamp(float x, float min, float max)		{ return (x < min)? min : (x > max)? max : x; }float frand(float x)							{ return (rand() / (float) RAND_MAX) * x; }float Pi()										{ static const float _Pi = (float)atan(1.0f) * 4.0; return _Pi; }struct Vector{	float x, y;	Vector()	{}	Vector(float _x, float _y)	: x(_x)	, y(_y)	{}	Vector& operator +=(const Vector& V) { x += V.x;  y += V.y; return *this; }	Vector& operator -=(const Vector& V) { x -= V.x;  y -= V.y; return *this; }	Vector& operator *=(float k)         { x *= k  ;  y *= k  ; return *this; }	Vector& operator /=(float k)         { x /= k  ;  y /= k  ; return *this; }			Vector operator + (const Vector& V) const { return Vector(x + V.x, y + V.y); }	Vector operator - (const Vector& V) const { return Vector(x - V.x, y - V.y); }	Vector operator * (float k)         const { return Vector(x * k, y * k); }	Vector operator / (float k)         const { return Vector(x / k, y / k); }		float  operator * (const Vector& V) const { return x * V.x + y * V.y; }	float  operator ^ (const Vector& V) const { return x * V.y - y * V.x; }	float	length() const { return (float)sqrt(x*x + y*y); }	float	normalise()    { float l = length(); if( l >0.0000001f) { x /= l; y /= l; } return l; }	Vector  normalised() const { Vector temp = *this; temp.normalise(); return temp; }		float   dotProduct	(const Vector& V) const { return (*this) * V; }	Vector  scale		(const Vector& xScale) const { return Vector(x * xScale.x,  y * xScale.y); }	Vector  invScale	(const Vector& xScale) const { return Vector(x / xScale.x,  y / xScale.y); }	Vector rotate(const Vector& C, float a) const	{		float px = (x - C.x) * (float)cos(a) - (y - C.y) * (float)sin(a) + C.x;		float py = (x - C.x) * (float)sin(a) + (y - C.y) * (float)cos(a) + C.y;		return Vector(px, py);	}	Vector& randomise(const Vector& Min, const Vector& Max)	{		x = Min.x + frand(Max.x - Min.x);		y = Min.y + frand(Max.y - Min.y);		return *this;	}};struct Colour{	float r;	float g;	float b;	float a;	Colour(float R, float G, float B, float A)	{		r = R;		g = G;		b = B;		a = A;	}	void render() const	{		glColor4f(r, g, b, a);	}};void renderPoint(const Vector& P, Colour col, float radius){	col.render();	glBegin(GL_POINTS);	glPointSize(radius);	glVertex2f(P.x, P.y);	glEnd();}void renderRectangle(const Vector& P, const Vector& H, Colour col, float radius){	col.render();	glBegin(GL_LINE_LOOP);	glLineWidth(radius);	glVertex2f(P.x - H.x, P.y - H.y);	glVertex2f(P.x + H.x, P.y - H.y);	glVertex2f(P.x + H.x, P.y + H.y);	glVertex2f(P.x - H.x, P.y + H.y);	glEnd();}void renderArrow(const Vector& P, const Vector& D, Colour col, float radius){	col.render();	glLineWidth(radius);		float angle = atan2(D.y, D.x);	glPushMatrix();	glTranslatef(P.x, P.y, 0.0f);	glScalef(D.length(), D.length(), 1.0f);	glRotatef(angle * 180.0f / Pi(), 0, 0, 1);	glBegin(GL_LINES);	glVertex2f(0, 0);	glVertex2f(1, 0);	glVertex2f(1, 0);	glVertex2f(0.9, -0.05);	glVertex2f(1, 0);	glVertex2f(0.9, +0.05);	glEnd();	glPopMatrix();}void renderCircle(const Vector& P, float r, Colour col, float radius){	col.render();	glLineWidth(radius);		glBegin(GL_LINE_LOOP);	int steps = 16;	float angle = 0.0;	for(int i = 0; i < steps; i ++, angle += (2.0 * Pi()) / (float) steps)	{		Vector D(cos(angle) * r, sin(angle) * r);		glVertex2f(P.x + D.x, P.y + D.y);	}	glVertex2f(P.x + r, P.y);		glEnd();}void update(float dt, Vector& velocity, Vector& position, const Vector& screenSize){	position += velocity * dt;	velocity *= 0.999f;	if(position.x < 0)		position.x = screenSize.x;	if(position.y < 0)		position.y = screenSize.y;	if(position.x > screenSize.x)		position.x = 0;	if(position.y > screenSize.y)		position.y = 0;}Vector closestPointOnRectangle(const Vector& point, const Vector& centre, const Vector& halfSize){    // relative position of sphere centre from the rectangle centre    Vector d = (point - centre);    // rectangle half-size    Vector h = halfSize;    // special case when the sphere centre is inside the rectangle    if(fabs(d.x) < h.x && fabs(d.y) < h.y)     {        // use left or right side of the rectangle boundary        // as it is the closest        if((h.x - fabs(d.x)) < (h.y - fabs(d.y)))        {             d.y = 0.0f;             d.x = h.x * sign(d.x);        }        // use top or bottom side of the rectangle boundary        // as it is the closest        else        {             d.x = 0.0f;             d.y = h.y * sign(d.y);        }    }    else    {        // clamp to rectangle boundary        if(fabs(d.x) > h.x) d.x = h.x * sign(d.x);        if(fabs(d.y) > h.y) d.y = h.y * sign(d.y);    }    // the closest point on rectangle from p    Vector c = centre + d;    return c;}bool rectangleRectangleColliding(const Vector& rect1Pos, const Vector& rect1HalfSize, const Vector& rect2Pos, const Vector& rect2HalfSize, Vector& mtd){	Vector min1 = rect1Pos - rect1HalfSize;	Vector max1 = rect1Pos + rect1HalfSize;	Vector min2 = rect2Pos - rect2HalfSize;	Vector max2 = rect2Pos + rect2HalfSize;	float dx0 = (max2.x - min1.x);	if(dx0 < 0) return false;	float dx1 = (max1.x - min2.x);	if(dx1 < 0) return false;	float dy0 = (max2.y - min1.y);	if(dy0 < 0) return false;	float dy1 = (max1.y - min2.y);	if(dy1 < 0) return false;	mtd = Vector(0, 0);	mtd.x = (dx0 < dx1)? dx0 : -dx1;	mtd.y = (dy0 < dy1)? dy0 : -dy1;	if(fabs(mtd.x) < fabs(mtd.y)) 		mtd.y = 0;	else		mtd.x = 0;	return true;}bool circleRectangleColliding(const Vector& sphereCentre, const float sphereRadius, const Vector& rectPos, const Vector& rectHalfSize, Vector& mtd){	Vector pointOnRectangle = closestPointOnRectangle(sphereCentre, rectPos, rectHalfSize);	Vector delta = (sphereCentre - pointOnRectangle);	float distanceSquared = (delta.dotProduct(delta));	if(distanceSquared > sphereRadius * sphereRadius)		return false;	Vector normal = delta / sqrt(distanceSquared);	Vector pointOnSphere = sphereCentre - normal * sphereRadius;		mtd = (pointOnRectangle - pointOnSphere);	renderPoint(pointOnRectangle, Colour(0, 1, 0, 1), 2);	renderPoint(pointOnSphere, Colour(0, 1, 0, 1), 2);	return true;}void intersectionResponse(Vector& pa, float ima, 						  Vector& pb, float imb, 						  const Vector& intersectionVector){	// separate the objects so they just touch each other    const float relaxation = 0.8f; // relaxation coefficient, arbitrary value in range [0, 1].    pa += intersectionVector * (ima / (ima + imb)) * relaxation;    pb -= intersectionVector * (imb / (ima + imb)) * relaxation;}void collisionResponse(Vector& va, float ima, 					   Vector& vb, float imb, 					   Vector& n){	// inverse masses (for static objects, inversemass = 0).    float im  = ima + imb;        // impact velocity along normal of collision 'n'    Vector v = (va - vb);    float vn = v.dotProduct(n);    // objects already separating, no reflection    if (vn > 0.0f) return;    const float cor = 0.7f; // coefficient of restitution. Arbitrary value, in range [0, 1].      // relative collision impulse    float j = -(1.0f + cor) * vn / (im);      // apply collision impulse to the two objects    va += n * (j * ima);    vb -= n * (j * imb);}int screen_width  = 640;int screen_height = 480;float framerate = 30.0f;struct Sphere{	Vector P;	Vector V;	float  r;	float  m;};struct Rect{	Vector P;	Vector H;	Vector V;	float  m;};// the rectangle (two vectors per rectangle, position, and halfsize).enum { MAX_RECTANGLES = 100 };int rectangleCount = 0;Rect rectangles[MAX_RECTANGLES];Sphere sphere;Vector mousePos(0, 0);//-------------------------------------------------------------------------------------------------////    OPENGL Functions////-------------------------------------------------------------------------------------------------void init(){	sphere.P.randomise(Vector(0, 0), Vector(screen_width, screen_height));	sphere.V = Vector(0, 0);	sphere.m = frand(30) + 10;	sphere.r = frand(20) + 10;		rectangleCount = rand() % 10 + 10;	for(int i = 0; i < rectangleCount; i ++)	{		rectangles.P.randomise(Vector(0, 0), Vector(screen_width, screen_height));		rectangles.H.randomise(Vector(screen_width / 100, screen_height / 100), Vector(screen_width / 20, screen_height / 20));		rectangles.V = Vector(0, 0);		rectangles.m = frand(30) + 10;	}}void display(void){	glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT);	glViewport(	0,  0, screen_width, screen_height);	glMatrixMode(GL_PROJECTION);	glLoadIdentity();	gluOrtho2D(0, screen_width, screen_height, 0);	glMatrixMode(GL_MODELVIEW);	glLoadIdentity();	// move spehre towards the mouse	Vector disp = mousePos - sphere.P;	float d = disp.length();	if(d > 5.0) disp *= 5.0f / d;	sphere.V += disp;	float dt = 1.0f / framerate;	// update sphere	update(dt, sphere.V, sphere.P, Vector(screen_width, screen_height));	// update rectangles		for(int i = 0; i < rectangleCount; i ++)	{		update(dt, rectangles.V, rectangles.P, Vector(screen_width, screen_height));	}	// collide sphere with rectangles	for(int i = 0; i < rectangleCount; i ++)	{		Vector mtd;		if(circleRectangleColliding(sphere.P, sphere.r, rectangles.P, rectangles.H, mtd))		{			intersectionResponse(sphere.P, 1.0f / sphere.m, rectangles.P, 1.0f / rectangles.m, mtd);			collisionResponse(sphere.V, 1.0f / sphere.m, rectangles.V, 1.0f / rectangles.m, mtd.normalised());		}	}	// collide rectangles against each other	for(int i = 0; i < rectangleCount; i ++)	{		for(int j = i+1; j < rectangleCount; j ++)		{						Vector mtd;			if(rectangleRectangleColliding(rectangles.P, rectangles.H, rectangles[j].P, rectangles[j].H, mtd))			{				intersectionResponse(rectangles.P, 1.0f / rectangles.m, rectangles[j].P, 1.0f / rectangles[j].m, mtd);				collisionResponse(rectangles.V, 1.0f / rectangles.m, rectangles[j].V, 1.0f / rectangles[j].m, mtd.normalised());			}		}	}	// render sphere	renderPoint(sphere.P, Colour(1, 0, 0, 1), 5);	renderPoint(mousePos, Colour(1, 0, 0, 1), 5);	renderCircle(sphere.P, sphere.r, Colour(1, 1.0, 1.0, 1), 2);	renderArrow(sphere.P, mousePos-sphere.P, Colour(1, 0.2, 0.2, 1), 1);		// render rectangles	for(int i = 0; i < rectangleCount; i ++)	{		renderPoint(rectangles.P, Colour(1, 0, 0, 1), 5);		renderRectangle(rectangles.P, rectangles.H, Colour(1, 1.0, 0.5, 1), 3);	}	glutSwapBuffers();}void reshape(int w,int h){	screen_width = w;	screen_height = h;}void ticker(int i){	display();	glutTimerFunc((int) (1000.0f / framerate), ticker, 0);}void keyboard(unsigned char key, int x, int y){	if(key == 27)	{		exit(0);	}	if(key == ' ')	{		init();	}}void mouse(int x, int y){	mousePos.x = x;	mousePos.y = y;}int main(int argc,char **argv){	glutInit(&argc,argv);	glutInitDisplayMode(GLUT_DOUBLE|GLUT_RGBA|GLUT_DEPTH);	glutInitWindowSize(screen_width, screen_height);	glutInitWindowPosition(100,100);	glutCreateWindow("verlet");	glutDisplayFunc(display);	glutReshapeFunc(reshape);	glutPassiveMotionFunc(mouse);	glutKeyboardFunc(keyboard);	glutTimerFunc((int) (1000.0f / framerate), ticker, 0);		glClearColor(0.0f,0.0f,0.3f,0.1f);	glPointSize(8);	glEnable(GL_POINT_SMOOTH);	glEnable(GL_LINE_SMOOTH);		glBlendFunc(GL_SRC_ALPHA,GL_ONE_MINUS_SRC_ALPHA);	glEnable(GL_BLEND);	init();	glutMainLoop();	return 0;}
Everything is better with Metal.
knonk
knonk
Yeah, Thanks a lot for your help, Oliii,finally i got what u meant, and I understood the basic method to process collision of two objects,Basic, we have 3 steps to process a collision, and that is :
1)First,We will find Collision normal vector in this step, collision between different pair of objects will have different way to find normal vector, but note that,in two next steps(2,3), we will process the same way for all objects collision.So go to step 2.
2)In this step,We have to process to separate 2 objects if they overlapped each other(also note that, in our collision detection method, we just know the collision happening when they'd collided already).
3)Finally,we have to process collision response as they are colliding in real case.
I did finish my demo and It's working very well.Thanks again Oliii, you did help me alot.
oliii
oliii
yep, that's the basics of it. Collision detection, and collision response are two different thing, given that the objects you test for collisions can be anything, but the collision response is applied on common properties (position tweaks to resolve intersections, and change in momentum to change their velocities).

so, you'd have a 'rigid body' class, with physical properties (position, velocity, mass), and in that body a reference to a base collision class, that is derived for spheres, rectangles, triangles and so on.

if you want more accurate collision detection, you need to 'sweep' volumes, which is more maths (and much more complicated if you want to take into account rotations). But collisions, or intersections, against any type of volume, will react with the same response code.

anyway, good to know you have it sussed.
Everything is better with Metal.
knonk
knonk
Follow your explanation,until now, I did make collision response with CIRCLES,RECTANGLES,WALLS. They were impacting to each other in a virtual physical world very well. I gonna add TRIANGLE to that world, but i think,actually, triangle is really a polygon with 3 edges and 3 vertexes, should i see it like a polygon, i will solve the collision problem between 2 polygons and the problem become more complicated. I have to find collision point to make MTD vector when 2 polygons collide each other. Seem there is not only one collision point here, maybe 1,or 2 or a ray with many collision points. So how can I find MTD vector in this situation, could you explain more for me, please.
oliii
oliii
you can do (convex) polygons using the SAT, or separating axis theorem.

It is explained here.

I've used a similar approach here.

The demoes / sandbox I have have a few steps in them. I've extended the SAT to do swept tests, contact point calculations, and rigid body dynamics, but the first few examples show the standard SAT for convex polygons, and how to get the MTD.
Everything is better with Metal.
knonk
knonk
Hi,Oliii. I did review ur code, in "Example 4 - Extending further for fast moving objects", you create CollisionInfo struct, something like this :
{....
// overlaps
bool m_overlapped;
float m_mtdLengthSquared;
Vector m_mtd;

// swept
bool m_collided;
Vector m_Nenter;
Vector m_Nleave;
float m_tenter;
float m_tleave;
}
Im sorry but I don't understand m_Nenter,m_Nleave,m_tenter,m_leave, what do they mean ? and what did u use it for ?

Topic Locked

This topic has been locked by a moderator. New replies are not allowed.

Sign in to reply to this topic.