k(u) = k(0)x(1-u) + k(1)x(u)
traditionally written with a single multiplication
k(u) = k(0) + ux(k(1) - k(0))
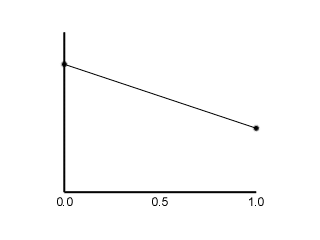 The most common method of interpolation. Certainly its speed of calculation is an advantage, but sharp changes of gradient at each keyframe can be visually disturbing. It creates the appearance of huge forces acting on the bone, or a lack of mass in the model.Cubic interpolation
The most common method of interpolation. Certainly its speed of calculation is an advantage, but sharp changes of gradient at each keyframe can be visually disturbing. It creates the appearance of huge forces acting on the bone, or a lack of mass in the model.Cubic interpolationk(u) = k(0)x(2u[sup]3[/sup]-3u[sup]2[/sup]+1) + k(1)x(3u[sup]2[/sup]-2u[sup]3[/sup])
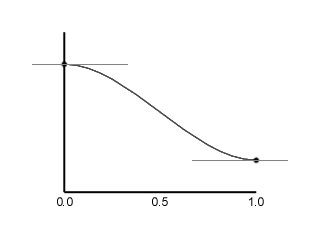 This interpolation overcomes the gradient change problem, as it has C(1) continuity (continuity of both position and gradient). However, it achieves this by reducing the gradient to zero at each keyframe, so the interpolation of a series of colinear values of k(t) would produce a curve with a peculiar oscillating gradient.Catmull-Rom spline interpolation
This interpolation overcomes the gradient change problem, as it has C(1) continuity (continuity of both position and gradient). However, it achieves this by reducing the gradient to zero at each keyframe, so the interpolation of a series of colinear values of k(t) would produce a curve with a peculiar oscillating gradient.Catmull-Rom spline interpolationRequires the gradients of the tangents at k(0) and k(1), denoted k'(0) and k'(1). Finding these tangents is explained below.
k(u) = k(0)x(2u[sup]3[/sup]-3u[sup]2[/sup]+1) +
k(1)x(3u[sup]2[/sup]-2u[sup]3[/sup]) +
k'(0)x(u[sup]3[/sup]-2u[sup]2[/sup]+u) +
k'(1)x(u[sup]3[/sup]-u[sup]2[/sup]) +
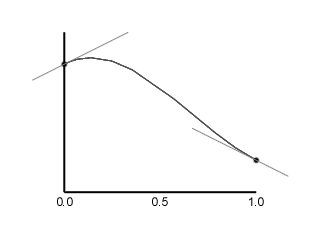 By modifying the cubic interpolation in this way, the curve can tend to a gradient other than 0. When an appropriate tangent is chosen, the resulting curve fits the keyframes very smoothly - with C(1) continuity, and no unnecessary points of inflexion.Finding the tangent gradients for the Catmull-Rom spline is quite straightforward:
k'(t) = 1/2 [k(t) - k(t-1)]/dx[sub]1[/sub] + 1/2 [k(t+1) - k(t)]/dx[sub]2[/sub]
In the case so far being examined, dx[sub]1[/sub] = dx[sub]2[/sub] = 1, as these are the intervals between keyframe values of t, and t is an integer. But what if keyframes could be placed at any value of t? This would certainly be beneficial for animators, as not all time intervals in an animation contain the same amount of "detail." In the few (very humble) animations I've made, I have found a constant trade-off between the amount of detail you would like one region of your animation to have, and the sheer number of keyframes piling up in your animation. Why not just put in keyframes where you need them, and have them smoothly interpolated while you're at it?
Another problem that this will assist with is when one part of an animation is running just a little too fast or too slow. To tweak this normally, you have to adjust all the frames around the area, but with this system, you can just slide a keyframe or two a tiny bit to correct the error.
This is an ability limited to high-end and non-realtime modelling software, as far as I know. Certainly, I've found no reference to coding it on the web.
[size="5"]Irregular keyframe timing
All that now remains is to adapt the interpolation to work with irregular keyframe intervals. We need a new array to store the time offset into the animation of each keyframe, denoted kt(i) for a particular keyframe i. The first change is in calculating the tangents - for example, moving keyframes together will obviously increase the slope of the tangent of the curve. The equation above becomes:
k'(t) = 1/2 [k(i) - k(i-1)]/[kt(i) - kt(i-1)] + 1/2 [k(t+1) - k(t)]/[kt(i) - kt(i-1)]
At the interpolation stage, we first need to find out what keyframes we're between at the moment. This is done easily enough with something like:
By modifying the cubic interpolation in this way, the curve can tend to a gradient other than 0. When an appropriate tangent is chosen, the resulting curve fits the keyframes very smoothly - with C(1) continuity, and no unnecessary points of inflexion.Finding the tangent gradients for the Catmull-Rom spline is quite straightforward:
k'(t) = 1/2 [k(t) - k(t-1)]/dx[sub]1[/sub] + 1/2 [k(t+1) - k(t)]/dx[sub]2[/sub]
In the case so far being examined, dx[sub]1[/sub] = dx[sub]2[/sub] = 1, as these are the intervals between keyframe values of t, and t is an integer. But what if keyframes could be placed at any value of t? This would certainly be beneficial for animators, as not all time intervals in an animation contain the same amount of "detail." In the few (very humble) animations I've made, I have found a constant trade-off between the amount of detail you would like one region of your animation to have, and the sheer number of keyframes piling up in your animation. Why not just put in keyframes where you need them, and have them smoothly interpolated while you're at it?
Another problem that this will assist with is when one part of an animation is running just a little too fast or too slow. To tweak this normally, you have to adjust all the frames around the area, but with this system, you can just slide a keyframe or two a tiny bit to correct the error.
This is an ability limited to high-end and non-realtime modelling software, as far as I know. Certainly, I've found no reference to coding it on the web.
[size="5"]Irregular keyframe timing
All that now remains is to adapt the interpolation to work with irregular keyframe intervals. We need a new array to store the time offset into the animation of each keyframe, denoted kt(i) for a particular keyframe i. The first change is in calculating the tangents - for example, moving keyframes together will obviously increase the slope of the tangent of the curve. The equation above becomes:
k'(t) = 1/2 [k(i) - k(i-1)]/[kt(i) - kt(i-1)] + 1/2 [k(t+1) - k(t)]/[kt(i) - kt(i-1)]
At the interpolation stage, we first need to find out what keyframes we're between at the moment. This is done easily enough with something like:
while (t >= kt[iKeyFrame+1]) iKeyFrame++;
Then we come across a slight snag - we need the value of u for the spline to work correctly. This is calculated as
u = (t - kt(i)) / (kt(i+1) - kt(i)).
The value (kt(i+1) - kt(i)) is actually used three times per interpolation, so I give it its own name, dx.
u = (t - kt(i)) / dx.
Of course, we've now scaled time, so while k(t) will hold, the tangent values k'(t) will be scaled by the same amount. We must replace k'() in the Catmull-Rom interpolation by k'() x dx. At first glance it may seem that this is the inverse operation to that performed when calculating the tangents, but it is not; both operations are necessary.
You now have your interpolated value of k(t). Apply this to your Euler angles, or your sleek slerped quaternions, and you will see some real smooth animation. Enjoy!
[size="5"]Glossary
k(t)
[bquote]The value of a keyframe at time t (one number, so several may be used to represent a complete orientation).[/bquote] k(u)
[bquote]The interpolated value between two values k(t) and k(t+1) (assuming a spacing of 1). u always takes a value in the range 0 to 1.[/bquote] k'(t)
[bquote]The "gradient" of a keyframe - this is not set by the user, as is the case with splines in many graphics programs, but is calculated as an average of the gradients of lines to the keyframes on either side.[/bquote] kt(i)
[bquote]The time value t for keyframe number i. It must always be the case that kt(i) < kt(i+1).[/bquote] dx
[bquote]The time interval between two particular keyframes. In most keyframing systems, dx is 1, or some constant value. In this system, dx can take any value, and can vary throughout the animation.[/bquote]

