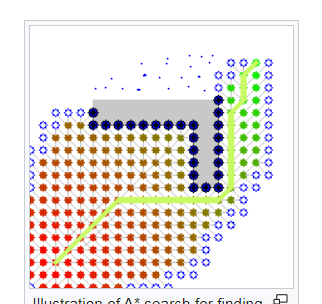
Alberth said:
It does? gScore seems to be the cost of the explored path to me.
Oh, you're right. Not sure why i got this wrong initially. Now it makes sense.
Alberth said:
What I don't know is if it ever happens that a better minimum real cost for a node ever occurs once you expanded the path from that node. It would need a path through that node with a shorter real cost, and thus a higher estimated cost than the path that reached that node you're expanding next. I guess it may happen if you have widely varying but always lower than real estimates but no idea what you need to ensure it never happens.
It's things like this why this stuff is difficult. I never trust myself to have thought on all special cases, and it's difficult to generate test data to clarify such doubts.
alvaro said:
In my particular implementation of the heuristic for this example, the true cost of moving to a neighbor is actually the same as what the heuristic returns, so I lazily used it.
I've noticed this one.
alvaro said:
it would be tricky to find it in the priority queue and update its cost. However, you can just add the node in the open list multiple times and make sure you don't process already closed nodes.
That's what i did for Dijkstra, with the ‘extracted’ bool vector.
I was using it for months before that, and only after that time i've noticed duplicates can happen, which caused my app to crash.
I did the fix with trial and error, not really understanding what i was doing. But duplicates went away, and it became faster as well, so i was happy. The resulting paths did not change.
But i was not sure this is guaranteed, or if some backtracking would be needed to do corrections. The Wikipedia articles also mentions an eventual need for a Fibonacci heap, or at least a requirement to update costs, which i did not.
This really seems the devilish detail here. It causes uncertainty, which needs to be resolved before making a fast real time implementation.